江苏省苏州市吴江区2020届九年级下学期数学第一次月考试卷
试卷更新日期:2020-04-20 类型:月考试卷
一、单选题
-
1. ﹣2020的绝对值是( )A、﹣2020 B、2020 C、﹣ D、2. 将 用科学记数法表示为( )A、 B、 C、 D、3. a,b都是实数,且a<b. 则下列不等式的变形正确的是( )A、 B、 C、 D、4. 下列关于0的说法正确的是( )A、0是正数 B、0是负数 C、0是有理数 D、0是无理数5.
如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )
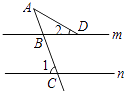 A、30° B、35° C、40° D、50°6. 若一个多边形的内角和与它的外角和相等,则这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形7. 已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形个数为( )
A、30° B、35° C、40° D、50°6. 若一个多边形的内角和与它的外角和相等,则这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形7. 已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形个数为( )
A、2 B、3 C、5 D、138. 一件毛衣先按成本提高50%标价,再以8折出售,获利70元,求这件毛衣的成本是多少元,若设成本是x元,可列方程为( )A、0.8x+70=(1+50%)x B、0.8 x-70=(1+50%)x C、x+70=0.8×(1+50%)x D、x-70=0.8×(1+50%)x9. 关于 的方程 有两个不相等的实数根,则实数 的取值范围是( )A、 B、 C、 且 D、 且10. 如图示,二次函数 的图像与 轴交于坐标原点和 ,若关于 的方程 ( 为实数)在 的范围内有解,则 的取值范围是( )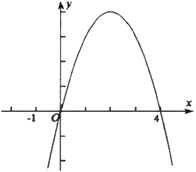 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算 =.12. 已知∠α=28°,则∠α的余角等于.13. 使根式 有意义的x的取值范围是 .14. 分式方程 的解是15. 如图,把矩形ABCD沿EF对折后使两部分重合,若∠1=50°,则∠AEF=
 16. 若 ,则 =.17. 如图,在平行四边形ABCD中,E为CB延长线上一点,且BE:CE=2:5,连接DE交AB于F,则 =
16. 若 ,则 =.17. 如图,在平行四边形ABCD中,E为CB延长线上一点,且BE:CE=2:5,连接DE交AB于F,则 = 18. 如图,已知 ,点 在边 上, .过点 作 于点 ,以 为一边在 内作等边 ,点 是 围成的区域(包括各边)内的一点,过点 作 交 于点 ,作 交 于点 .设 , ,则 最大值是.
18. 如图,已知 ,点 在边 上, .过点 作 于点 ,以 为一边在 内作等边 ,点 是 围成的区域(包括各边)内的一点,过点 作 交 于点 ,作 交 于点 .设 , ,则 最大值是.
三、解答题
-
19. .20. 先化简,再求值: ,其中 .21. 解不等式组 ,并将解集在数轴上表示出来.
 22. 如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
22. 如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.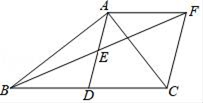 (1)、求证:△AEF≌△DEB;(2)、若∠BAC=90°,求证:四边形ADCF是菱形.23. 如图,在由边长为1个单位长度的小正方形组成的网格图中,△ABC的顶点都在网格线交点上.
(1)、求证:△AEF≌△DEB;(2)、若∠BAC=90°,求证:四边形ADCF是菱形.23. 如图,在由边长为1个单位长度的小正方形组成的网格图中,△ABC的顶点都在网格线交点上.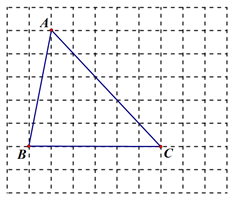 (1)、图中AC边上的高为个单位长度;(2)、只用没有刻度的直尺,在所给网格图中按如下要求画图(保留必要痕迹):
(1)、图中AC边上的高为个单位长度;(2)、只用没有刻度的直尺,在所给网格图中按如下要求画图(保留必要痕迹):①以点C为位似中心,把△ABC按相似比1:2缩小,得到△DEC;
②以AB为一边,作矩形ABMN,使得它的面积恰好为△ABC的面积的2倍.
24. 为了丰富校园文化生活,促进学生积极参加体育运动,某校准备成立校排球队,现计划购进一批甲、乙两种型号的排球,已知一个甲种型号排球的价格与一个乙种型号排球的价格之和为140元;如果购买6个甲种型号排球和5个乙种型号排球,一共需花费780元.(1)、求每个甲种型号排球和每个乙种型号排球的价格分别是多少元?(2)、学校计划购买甲、乙两种型号的排球共26个,其中甲种型号排球的个数多于乙种型号排球,并且学校购买甲、乙两种型号排球的预算资金不超过1900元,求该学校共有几种购买方案?25. 如图,边长为2的正方形 的顶点 在 轴正半轴上,反比例函数 的图像在第一象限的图像经过点 ,交 于 . (1)、当点 的坐标为 时,求 和 的值;(2)、若 ,求 的面积.26. 已知函数 ( 是常数)(1)、当 时,该函数图象与直线 有几个公共点?请说明理由;(2)、若函数图象与 轴只有一公共点,求 的值.27. 如图①,四边形 是矩形, ,点 是线段 上一动点 (不与 重合),点 是线段 延长线上一动点,连接 交 于点 .设 ,已知 与 之间的函数关系如图②所示.
(1)、当点 的坐标为 时,求 和 的值;(2)、若 ,求 的面积.26. 已知函数 ( 是常数)(1)、当 时,该函数图象与直线 有几个公共点?请说明理由;(2)、若函数图象与 轴只有一公共点,求 的值.27. 如图①,四边形 是矩形, ,点 是线段 上一动点 (不与 重合),点 是线段 延长线上一动点,连接 交 于点 .设 ,已知 与 之间的函数关系如图②所示.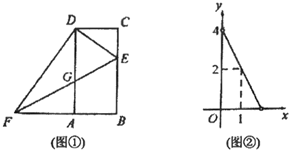 (1)、求图②中 与 的函数表达式;(2)、求证: ;(3)、是否存在 的值,使得 是等腰三角形?如果存在,求出 的值;如果不存在,说明理由.28. 如图示,在平面直角坐标系中,二次函数 ( )交 轴于 , ,在 轴上有一点 ,连接 .
(1)、求图②中 与 的函数表达式;(2)、求证: ;(3)、是否存在 的值,使得 是等腰三角形?如果存在,求出 的值;如果不存在,说明理由.28. 如图示,在平面直角坐标系中,二次函数 ( )交 轴于 , ,在 轴上有一点 ,连接 .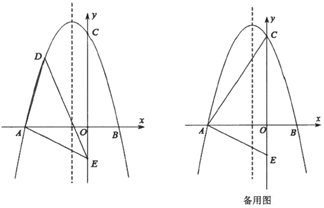 (1)、求二次函数的表达式;(2)、点 是第二象限内的点抛物线上一动点
(1)、求二次函数的表达式;(2)、点 是第二象限内的点抛物线上一动点①求 面积最大值并写出此时点 的坐标;
②若 ,求此时点 坐标;
(3)、连接 ,点 是线段 上的动点.连接 ,把线段 绕着点 顺时针旋转 至 ,点 是点 的对应点.当动点 从点 运动到点 ,则动点 所经过的路径长等于(直接写出答案)