河南省南阳市镇平县2020届九年级下学期数学3月月考试卷
试卷更新日期:2020-04-20 类型:月考试卷
一、单选题
-
1. 下列约分正确的是( )A、 =x3; B、 ; C、 ; D、2. 二次函数y=x2+4x-5的图象的对称轴为( )A、x=4 B、x=-4 C、x=2 D、x=-23. 若分式 的值为零,则x=( )A、3 B、-3 C、±3 D、04. 无论m为任何实数,关于x的一次函数y=x+2m与y=-x+4的图象的交点一定不在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,在△ABC中,∠A=90°,AB=3,BC=5,则cosB等于( )
 A、 B、 C、 D、6. 表格列出了一项实验的统计数据,表示皮球从高度d落下时弹跳高度b与下落高d的关系,试问下面的哪个式子能表示这种关系(单位cm)( )
A、 B、 C、 D、6. 表格列出了一项实验的统计数据,表示皮球从高度d落下时弹跳高度b与下落高d的关系,试问下面的哪个式子能表示这种关系(单位cm)( )d
50
80
100
150
b
25
40
50
75
A、 B、 C、 D、7. 如图,某风景区为了方便游人参观,计划从主峰A处架设一条缆车线路到另一山峰C处,若在A处测得C处的俯角为30°,两山峰的底部BD相距900米,则缆车线路AC的长为( )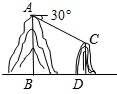 A、300 米 B、600 米 C、900 米 D、1800米8. 将抛物线 向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线解析式为( )A、 B、 C、 D、9. 在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是( )A、
A、300 米 B、600 米 C、900 米 D、1800米8. 将抛物线 向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线解析式为( )A、 B、 C、 D、9. 在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是( )A、 B、
B、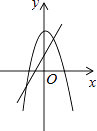 C、
C、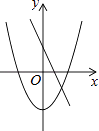 D、
D、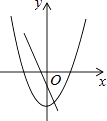 10. 某工厂现在平均每天比原计划多生产50台机器,现在生产800台机器所需时间与原计划生产600台机器所需时间相同.设原计划平均每天生产x台机器,根据题意,下面所列方程正确的是( )A、 B、 C、 D、
10. 某工厂现在平均每天比原计划多生产50台机器,现在生产800台机器所需时间与原计划生产600台机器所需时间相同.设原计划平均每天生产x台机器,根据题意,下面所列方程正确的是( )A、 B、 C、 D、二、填空题
-
11. 化简: .12. 如图,O是坐标原点,边长为2的菱形OABC的顶点C在x轴的负半轴上,cos∠AOC= ,函数 的图象经过顶点B,则k的值为.
 13. 小聪家对面新建了一幢图书大厦,他在A处测得点D的俯角α为30°,测得点C的俯角β为60°(如图所示),量得两幢楼之间的水平距离BC为30米,则图书大厦CD的高度为米.
13. 小聪家对面新建了一幢图书大厦,他在A处测得点D的俯角α为30°,测得点C的俯角β为60°(如图所示),量得两幢楼之间的水平距离BC为30米,则图书大厦CD的高度为米.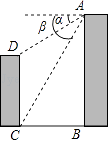 14. 如图所示,在矩形ABCD中,动点P从点B出发,沿BC , CD , DA运动至点A停止,设点P运动的路程为 ,△ABP的面积为 ,如果 关于 的函数图象如图所示,那么△ABC的面积是.
14. 如图所示,在矩形ABCD中,动点P从点B出发,沿BC , CD , DA运动至点A停止,设点P运动的路程为 ,△ABP的面积为 ,如果 关于 的函数图象如图所示,那么△ABC的面积是.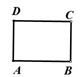
 15. 如图,在△ABC中,∠C=90°,AC=8,BC=6,点D是AB的中点,点E在AC上,将△ADE沿DE翻折,使点A落在点A′处,当A′D与△ABC的一边平行时,A′B=.
15. 如图,在△ABC中,∠C=90°,AC=8,BC=6,点D是AB的中点,点E在AC上,将△ADE沿DE翻折,使点A落在点A′处,当A′D与△ABC的一边平行时,A′B=.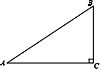
三、解答题
-
16. 解分式方程: .17. 已知二次函数y=x2-2mx+m2+3(m是常数).(1)、求证:不论m为何值,该函数的图象与x轴没有公共点;(2)、把该函数的图象沿y轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点?18. 先化简,再求值: ,其中整数x与2、3构成△ABC的三条边长.19. 五一期间,小明随父母到某旅游胜地参观游览,他在游客中心O处测得景点A在其北偏东72°方向,测得景点B在其南偏东40°方向.小明从游客中心走了2千米到达景点A,已知景点B正好位于景点A的正南方向,求景点A与B之间的距离.(结果精确到0.1千米)
(参考数据:sin72°≈0.95,cos72°≈0.31,sin40°≈0.64,tan40°≈0.84)
 20. 如图,反比例函数 与一次函数 的图象交于两点A(1,3)、B(n,-1).
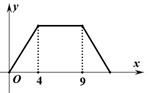
20. 如图,反比例函数 与一次函数 的图象交于两点A(1,3)、B(n,-1).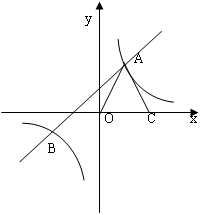 (1)、求这两个函数的解析式;(2)、观察图象,请直接写出不等式 的解集;(3)、点C为x轴正半轴上一点,连接AO、AC,且AO=AC,求⊿AOC的面积.21. 某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)、求这两个函数的解析式;(2)、观察图象,请直接写出不等式 的解集;(3)、点C为x轴正半轴上一点,连接AO、AC,且AO=AC,求⊿AOC的面积.21. 某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.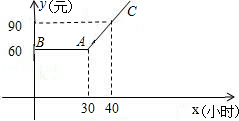 (1)、当x≥30,求y与x之间的函数关系式;(2)、若小李4月份上网20小时,他应付多少元的上网费用?(3)、若小李5月份上网费用为75元,则他在该月份的上网时间是多少?22. 如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:≈1.414,≈1.732)
(1)、当x≥30,求y与x之间的函数关系式;(2)、若小李4月份上网20小时,他应付多少元的上网费用?(3)、若小李5月份上网费用为75元,则他在该月份的上网时间是多少?22. 如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:≈1.414,≈1.732)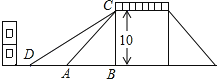 23. 如图,直线 与x轴交于点A(3,0),与y轴交于点B,抛物线 经过点A,B.
23. 如图,直线 与x轴交于点A(3,0),与y轴交于点B,抛物线 经过点A,B. (1)、求点B的坐标和抛物线的解析式;(2)、M(m,0)为线段OA上一个动点,过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
(1)、求点B的坐标和抛物线的解析式;(2)、M(m,0)为线段OA上一个动点,过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N.①试用含m的代数式表示PN的长;
②m为何值时△ABN面积最大,并求△ABN的最大值.