浙江省台州市黄岩区2020年九年级下学期数学期中考试试卷
试卷更新日期：2020-04-20 类型：期中考试
一、单选题
-
1. ﹣|﹣3|的倒数是（ ）A、﹣3 B、﹣ C、 D、32. 第二届“一带一路”国际合作高峰论坛于2019年4月25日至27日在北京召开，“一带一路”建设进行5年多来，中资金融机构为“一带一路”相关国家累计发放贷款250000000000元，重点支持了基础设施、社会民生等项目．数字250000000000用科学记数法表示，正确的是（ ）A、0.25×1011 B、2.5×1011 C、2.5×1010 D、25×10103. 四边形ABCD中，对角线AC、BD相交于O，如果AO＝CO，BO＝DO，AC⊥BD，那么这个四边形（ ）A、仅是轴对称图形 B、仅是中心对称图形 C、既是轴对称图形，又是中心对称图形 D、以上都不对4. 把一副三角板放在同一水平桌面上，摆放成如图所示的形状，使两个直角顶点重合，两条斜边平行，则∠1的度数是（ ）
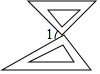A、45° B、60° C、75° D、82.5°5. 某住宅小区六月份1日至5日每天用水量变化情况如图所示．那么这5天用水量的中位数是（ ）
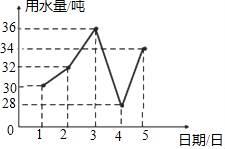A、30吨 B、36吨 C、32吨 D、34吨6. 学校组织校外实践活动，安排给九年级两辆车，小明与小慧都可以从两辆车中任选一辆搭乘，则小明和小慧乘同一辆车的概率是（ ）.A、 B、 C、 D、17. 如图，AB是半圆的直径，O为圆心，C是半圆上的点，D是 上的点，若∠BOC=40°，则∠D的度数为（ ）
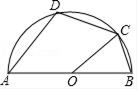A、100° B、110° C、120° D、130°8. 若0＜m＜2，则关于x的一元二次方程﹣（x+m）（x+3m）＝3mx+37根的情况是（ ）A、无实数根 B、有两个正根 C、有两个根，且都大于﹣3m D、有两个根，其中一根大于﹣m9. 如图所示，在△ABC中，内角∠BAC与外角∠CBE的平分线相交于点P，BE＝BC，PB与CE交于点H，PG∥AD交BC于F，交AB于G，连接CP．下列结论：①∠ACB＝2∠APB；②S△PAC：S△PAB＝AC：AB；③BP垂直平分CE；④∠PCF＝∠CPF．其中，正确的有（ ）
A、1个 B、2个 C、3个 D、4个10. 如图1，正方形ABCD在直角坐标系中，其中AB边在y轴上，其余各边均与坐标轴平行，直线l：y＝x﹣5沿y轴的正方向以每秒1个单位的速度平移，在平移的过程中，该直线被正方形ABCD的边所截得的线段长为m，平移的时间为t（秒），m与t的函数图象如图2所示，则图2中b的值为（ ）
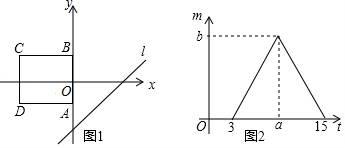A、3 B、5 C、6 D、10二、填空题
-
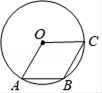
11. 因式分解：9a3b﹣ab＝.12. 如图，菱形OABC的边长为2，且点A、B、C在⊙O上，则劣弧 的长度为.
13. 定义一种新运算：a※b＝ ，则2※3﹣4※3的值.14. 如图，在Rt△ABC中，∠C＝90°，BC＝4，BA＝5，点D是边AC上的一动点，过点D作DE∥AB交边BC于点E，过点B作BF⊥BC交DE的延长线于点F，分别以DE，EF为对角线画矩形CDGE和矩形HEBF，则在D从A到C的运动过程中，当矩形CDGE和矩形HEBF的面积和最小时，AD的长度为 ．
15. 如图，把矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y轴上，连接OB，将纸片OABC沿OB折叠，使点A落在点A′的位置，若OB＝ ，tan∠BOC＝ ，则点A′的坐标为.
16. 如图，点A，B为定点，直线l∥AB，P是l上一动点，点M，N分别为PA，PB的中点，对于下列各值：①线段MN的长；②△PAB的周长；③△PMN的面积；④直线MN与AB之间的距离；⑤∠APB的大小．其中会随点P的移动而发生变化的是（填序号）．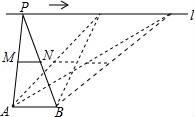
三、解答题
-
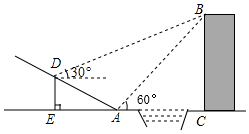
17. 已知：（x﹣1）（x+3）＝ax2+bx+c，求代数式9a﹣3b+c的值．18. 解不等式组： ，并写出该不等式组的整数解．19. 如图，某中学数学活动小组在学习了“利用三角函数测高”后，选定测量小河对岸一幢建筑物BC的高度，他们先在斜坡上的D处，测得建筑物顶端B的仰角为30°．且D离地面的高度DE＝5m．坡底EA＝30m，然后在A处测得建筑物顶端B的仰角是60°，点E，A，C在同一水平线上，求建筑物BC的高．(结果用含有根号的式子表示)
20. 如图，在平面直角坐标系xOy中，直线y=x﹣2与双曲线y= (k≠0)相交于A，B两点，且点A的横坐标是3.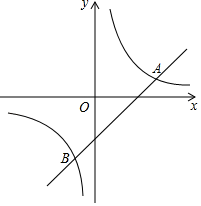
(1)、求k的值；(2)、过点P(0，n)作直线，使直线与x轴平行，直线与直线y=x﹣2交于点M，与双曲线y= (k≠0)交于点N，若点M在N右边，求n的取值范围.21. 某中学对本校初2018届500名学生中中考参加体育加试测试情况进行调查，根据男生1000米及女生800米测试成绩整理，绘制成不完整的统计图，(图①，图②)，根据统计图提供的信息，回答问题：
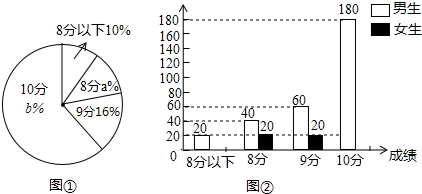(1)、该校毕业生中男生有人；扇形统计图中 ；(2)、扇形统计图中，成绩为10分的所在扇形的圆心角是多少度？并补全条形统计图；(3)、若500名学生中随机抽取一名学生，这名学生该项成绩在8分及8分以下的概率是多少？22. 已知△ABC是边长为4的等边三角形，边AB在射线OM上，且OA＝6，点D是射线OM上的动点，当点D不与点A重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE，连接DE，设OD＝m．
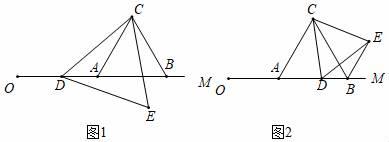(1)、问题发现如图1，△CDE的形状是三角形．
(2)、探究证明如图2，当6＜m＜10时，△BDE的周长是否存在最小值？若存在，求出△BDE周长的最小值；若不存在，请说明理由．
(3)、解决问题是否存在m的值，使△DEB是直角三角形？若存在，请直接写出m的值；若不存在，请说明理由．
23. 甲、乙两人相约周末登花果山，甲、乙两人距地面的高度y（米）与登山时间x（分）之间的函数图象如图所示，根据图象所提供的信息解答下列问题：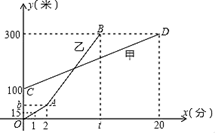
(1)、甲登山上升的速度是每分钟米，乙在A地时距地面的高度b为米；(2)、若乙提速后，乙的登山上升速度是甲登山上升速度的3倍，请求出乙登山全程中，距地面的高度y（米）与登山时间x（分）之间的函数关系式；(3)、登山多长时间时，甲、乙两人距地面的高度差为70米？24. 如图1，在矩形ABCD中，AB＝8，AD＝10，E是CD边上一点，连接AE，将矩形ABCD沿AE折叠，顶点D恰好落在BC边上点F处，延长AE交BC的延长线于点G．
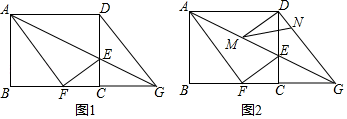(1)、求线段CE的长；(2)、如图2，M，N分别是线段AG，DG上的动点（与端点不重合），且∠DMN＝∠DAM，设AM＝x，DN＝y．①写出y关于x的函数解析式，并求出y的最小值；
②是否存在这样的点M，使△DMN是等腰三角形？若存在，请求出x的值；若不存在，请说明理由．