人教A版(2019)数学必修第二册 第六章平面向量及其应用
试卷更新日期:2020-04-19 类型:单元试卷
一、单选题
-
1. 已知向量 , 满足 , 则 ( )A、 B、 C、 D、2. 在 ABC中,角A , B , C所对的边分别为a , b , c.若 , , ,则 ABC的面积等于( )A、 或 B、 C、 D、3. 在△ 中, , ,则 等于( )A、 B、 C、 D、94. 已知向量 =(1,0), =(-3,4)的夹角为 ,则sin2 等于 ( )A、 B、 C、 D、5. 已知向量 , ,若 ,则实数 ( )A、 B、 C、3 D、
 6. 已知向量 ,则 的充要条件是 ( )A、 B、 C、 D、7. 已知向量 , 的夹角为60°, , ,则 ( )A、2 B、 C、 D、18. 在 中, 为 边上的中线,点 满足 ,则 ( )A、 B、 C、 D、9. 已知 , ,若 ,则 的取值范围为( )A、 B、 C、 D、10. 已知向量 , 满足 , , ,那么 与 的夹角为( )A、 B、 C、 D、11. 已知非零向量 , 满足 ,且 ,则 与 的夹角为( )A、 B、 C、 D、12. 中所在的平面上的点 满足 ,则 ( )A、 B、 C、 D、13. 若向量 与向量 满足:| |=2,| |=3,且当λ∈R时,| |的最小值为2 ,则向量 在向量 方向上的投影为( )A、1 或2 B、2 C、1 或3 D、314. 中, , , ,点 是 内(包括边界)的一动点,且 ,则 的最小值是( )A、 B、 C、3 D、15. 蓝军和红军进行军事演练,蓝军在距离 的军事基地 和 ,测得红军的两支精锐部队分别在 处和 处,且 , , , ,如图所示,则红军这两支精锐部队间的距离是 ( )
6. 已知向量 ,则 的充要条件是 ( )A、 B、 C、 D、7. 已知向量 , 的夹角为60°, , ,则 ( )A、2 B、 C、 D、18. 在 中, 为 边上的中线,点 满足 ,则 ( )A、 B、 C、 D、9. 已知 , ,若 ,则 的取值范围为( )A、 B、 C、 D、10. 已知向量 , 满足 , , ,那么 与 的夹角为( )A、 B、 C、 D、11. 已知非零向量 , 满足 ,且 ,则 与 的夹角为( )A、 B、 C、 D、12. 中所在的平面上的点 满足 ,则 ( )A、 B、 C、 D、13. 若向量 与向量 满足:| |=2,| |=3,且当λ∈R时,| |的最小值为2 ,则向量 在向量 方向上的投影为( )A、1 或2 B、2 C、1 或3 D、314. 中, , , ,点 是 内(包括边界)的一动点,且 ,则 的最小值是( )A、 B、 C、3 D、15. 蓝军和红军进行军事演练,蓝军在距离 的军事基地 和 ,测得红军的两支精锐部队分别在 处和 处,且 , , , ,如图所示,则红军这两支精锐部队间的距离是 ( )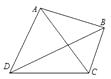 A、 B、 C、 D、16. 一艘客船上午9:30在A处,测得灯塔S在它的北偏东30°,之后它以每小时32海里的速度继续沿正北方向匀速航行,上午10:00到达B处,此时测得船与灯塔S相距8 海里,则灯塔S在B处的( )
A、 B、 C、 D、16. 一艘客船上午9:30在A处,测得灯塔S在它的北偏东30°,之后它以每小时32海里的速度继续沿正北方向匀速航行,上午10:00到达B处,此时测得船与灯塔S相距8 海里,则灯塔S在B处的( )
A、北偏东75° B、北偏东75°或东偏南75° C、东偏南75° D、以上方位都不对二、填空题
-
17. 已知向量 , ,且 ,则18. 已知向量 , 满足 , ,若 ,则 与 的夹角为.19. 如图,在单位圆 中, 为圆上的一个定点, 为圆上的一个动点, 的取值范围为.
 20. 如图所示,在平面四边形 中, , , 为正三角形,则 面积的最大值为 .
20. 如图所示,在平面四边形 中, , , 为正三角形,则 面积的最大值为 .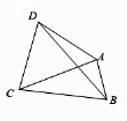
三、解答题