人教A版（2019）数学必修第二册 6.4平面向量的应用

试卷更新日期：2020-04-19 类型：同步测试

进入出卷网下载

一、单选题

1. 已知 $Δ A B C$ 的外接圆半径是2， $A = 60^{\circ}$ ，则 $B C =$ （）

A、 $\frac{\sqrt{3}}{2}$ B、 $2 \sqrt{3}$ C、 $\sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
2. 在 $△ A B C$ 中，角 $A ， B ， C$ 所对的边分别为 $a ， b ， c$ ，若 $a = 1$ ，b= $\sqrt{7}$ ， $c = \sqrt{3}$ ，则 $B =$ （）

A、 $\frac{π}{6}$ B、 $\frac{5π}{6}$ C、 $\frac{5π}{6}$ 或 $\frac{π}{6}$ D、 $\frac{π}{3}$

查看试题解析
3. 已知 $Δ A B C$ 的三个内角 $A, B, C$ 的对边分别为 $a, b, c$ ，且满足 $a \cos B + b \cos A = - c \sqrt{2} \cos A$ ，则 $A$ 等于（）

A、 $\frac{π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{3 π}{4}$

查看试题解析
4. 设点 $G$ 是 $Δ A B C$ 的重心，且满足 $2 \sin B \cdot \vec{A B} + 3 \sin A \cdot \vec{G A} + 2 \sin C \cdot \vec{G C} = \vec{0}$ ，则 $\cos C =$ （）

A、 $\frac{3}{4}$ B、 $\frac{2}{3}$ C、 $\frac{1}{3}$ D、 $\frac{9}{16}$

查看试题解析
5. 在 $△ A B C$ 中，D是边AC上的点，且 $A B = A D ，$ $2 A B = \sqrt{3} B D ，$ $B C = 2 B D$ ，则 $\sin C$ 的值为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{3}}{6}$ C、 $\frac{\sqrt{6}}{4}$ D、 $\frac{\sqrt{6}}{6}$

查看试题解析
6. 如图，《九章算术》中记载了一个“折竹抵地”问题：今有竹高一丈，末折抵地，去本三尺，问折者高几何？意思是：有一根竹子原高一丈（一丈 $= 10$ 尺），现被风折断，尖端落在地上，竹尖与竹根的距离三尺，问折断处离地面的高是（）

A、2.55尺 B、4.55尺 C、5.55尺 D、6.55尺

查看试题解析
7. 如图，从地面上C，D两点望山顶A，测得它们的仰角分别为45°和30°，已知CD＝100米，点C位于BD上，则山高AB等于（）

A、 $50 (\sqrt{3} + 1)$ 米 B、 $50 \sqrt{3}$ 米 C、 $50 \sqrt{2}$ 米 D、100米

查看试题解析
8. 一船以每小时 $15 \sqrt{2}$ km的速度向东行驶，船在A处看到一灯塔B在北偏东60°，行驶4小时后，船到达C处，看到这个灯塔在北偏东15°，这时船与灯塔的距离为（）

A、60km B、 $60 \sqrt{2}$ km C、 $30 \sqrt{2}$ km D、30km

查看试题解析
9. 在 $Δ A B C$ 中，角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，若 $\frac{sin A}{k} = \frac{sin B}{3} = \frac{sin C}{4}$ （ $k$ 为非零实数），则下列结论错误的是（）

A、当 $k = 5$ 时， $Δ A B C$ 是直角三角形 B、当 $k = 3$ 时， $Δ A B C$ 是锐角三角形 C、当 $k = 2$ 时， $Δ A B C$ 是钝角三角形 D、当 $k = 1$ 时， $Δ A B C$ 是钝角三角形

查看试题解析
10. 如图，飞机的航线和山顶在同一个铅垂平面内，已知飞机的高度为海拔 $20000$ m，速度为 $900$ km/h，飞行员先看到山顶的俯角为 $30^{\circ}$ ，经过80s后又看到山顶的俯角为 $75^{\circ}$ ，则山顶的海拔高度为（）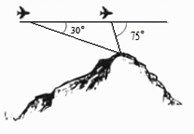

A、 $5000 (\sqrt{3} + 1) m$ B、 $5000 (\sqrt{3} - 1) m$ C、 $5000 (3 - \sqrt{3}) m$ D、 $5000 (5 - \sqrt{3}) m$

查看试题解析
11. 如图，巡航艇在海上以 $60 km / h$ 的速度沿南偏东 $40 °$ 的方向航行．为了确定巡航艇的位置，巡航艇在B处观测灯塔A，其方向是南偏东 $70 °$ ，航行 $\frac{1}{2} h$ 到达C处，观测灯塔A的方向是北偏东 $65 °$ ，则巡航艇到达C处时，与灯塔A的距离是

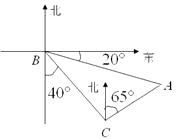A、 $10 km$ B、 $10 \sqrt{2} km$ C、 $15 km$ D、 $15 \sqrt{2} km$

查看试题解析
12. 为绘制海底地貌图，测量海底两点C，D间的距离，海底探测仪沿水平方向在，两点进行测量，，，，在同一个铅垂平面内. 海底探测仪测得
，两点的距离为海里，求的面积( )平方海里。

A、 B、 C、 D、

查看试题解析

二、填空题

13. $Δ A B C$ 中， $A C = 6$ ， $B C = 2 A B$ ， $B = \frac{π}{3}$ ，则 $A B =$ .

查看试题解析
14. 在 $△ A B C$ 中，若 $A = 30 °$ ， $B = 120 °$ ， $b = 12$ ，则 $a =$ .

查看试题解析
15. 如图所示，在山脚 $A$ 测得山顶 $P$ 的仰角为 $∠ Q A P = 45^{\circ}$ ，沿倾斜角为 $∠ Q A B = 15^{\circ}$ 的斜坡向上走146.4米到达 $B$ ，在 $B$ 测得山顶 $P$ 的仰角为 $∠ C B P = 60^{\circ}$ ，则山高 $P Q =$ 米．（ $\sqrt{2} = 1.414$ ， $\sqrt{3} = 1.732$ ，结果保留小数点后1位）

查看试题解析
16. 某舰艇在 $A$ 处测得遇险渔船在北偏东 $45 °$ 方向上的 $C$ 处，且到 $A$ 的距离为 $10$ 海里，此时得知，该渔船沿南偏东 $75 °$ 方向，以每小时 $9$ 海里的速度向一小岛靠近，舰艇的速度为 $21$ 海里/小时，则舰艇到达渔船的最短时间是小时．

查看试题解析

三、解答题

17. 已知 $Δ A B C$ 的内角 $A$ ､ $B$ ､ $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ，且 $a = 2 \sqrt{3}$ .

(1)、若 $b = 2$ ，角 $A = 60 °$ ，求角 $B$ 的值；

(2)、若 $S_{Δ A B C} = 3$ ， $\cos B = \frac{4}{5}$ ，求 $b$ ， $c$ 的值.

查看试题解析
18. 在 $Δ A B C$ 中，三边 $a$ ， $b$ ， $c$ 的对角分别为 $A$ ， $B$ ， $C$ ，已知 $a = 3$ ， $\frac{\cos B + \cos A \cos C}{\sin B \cos C} = \frac{\sqrt{3} a}{b}$ .

(1)、若 $c = 2 \sqrt{3}$ ，求 $\sin A$ ；

(2)、若 $A B$ 边上的中线长为 $\frac{\sqrt{37}}{2}$ ，求 $Δ A B C$ 的面积.

查看试题解析
19. 已知数列 ${a_{n}}$ 的前 $n$ 项和 $S_{n} = \frac{n^{2} + n}{2} .$

(1)、若三角形的三边长分别为 $a_{3} 、 a_{5} 、 a_{7} ，$ 求此三角形的面积；

(2)、探究数列 ${a_{n}}$ 中是否存在相邻的三项，同时满足以下两个条件：
①此三项可作为三角形三边的长；

②此三项构成的三角形最大角是最小角的2倍.

若存在，找出这样的三项；若不存在，说明理由.

查看试题解析
20. 东西向的铁路上有两个道口 $A$ 、 $B$ ，铁路两侧的公路分布如图， $C$ 位于 $A$ 的南偏西 $15^{°}$ ，且位于 $B$ 的南偏东 $15^{°}$ 方向， $D$ 位于 $A$ 的正北方向， $A C = A D = 2 k m$ ， $C$ 处一辆救护车欲通过道口前往 $D$ 处的医院送病人，发现北偏东 $45^{°}$ 方向的 $E$ 处(火车头位置)有一列火车自东向西驶来，若火车通过每个道口都需要 $1$ 分钟，救护车和火车的速度均为 $60 k m / h$ .

(1)、判断救护车通过道口 $A$ 是否会受火车影响，并说明理由；

(2)、为了尽快将病人送到医院，救护车应选择 $A$ 、 $B$ 中的哪个道口？通过计算说明.

查看试题解析