西藏自治区日喀则市三校2019-2020学年高三上学期文数11月月考试卷
试卷更新日期:2020-04-17 类型:月考试卷
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. 已知复数 满足 ,则 的虚部为( )A、-4 B、 C、4 D、3. 已知 , 则的值为( )
A、 B、 C、 D、4. 已知椭圆 上的一点 到椭圆一个焦点的距离为 ,则 到另一焦点距离( )A、2 B、3 C、5 D、75. 已知| |=1,| |= ,且 ,则向量 与向量 的夹角为( )A、 B、 C、 D、6. 若 是 的三个内角的对边,且 ,则圆 : 被直线 : 所截得的弦长为( )A、 B、 C、6 D、57. 若实数 满足 则 的最小值是( )A、0 B、1 C、 . D、98. 在数列 中, , ,则 ( )A、 B、 C、 D、9. 函数 , 则 ( )A、-3 B、-2 C、-1 D、010. 阅读如图所示的程序框图,运行相应的程序.若输出的S为 ,则判断框中填写的内容可以是( )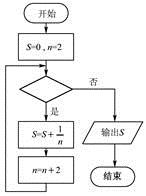 A、 B、 C、 D、11. 抛物线 上的一点 到焦点的距离为1,则点 的纵坐标是( )A、 B、1 C、 D、12. 一只蚂蚁从正方体 的顶点 出发,经正方体的表面,按最短路线爬行到顶点 的位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图的是( )
A、 B、 C、 D、11. 抛物线 上的一点 到焦点的距离为1,则点 的纵坐标是( )A、 B、1 C、 D、12. 一只蚂蚁从正方体 的顶点 出发,经正方体的表面,按最短路线爬行到顶点 的位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图的是( )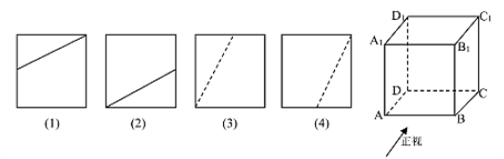 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 在等差数列 中,已知 a4+a8=16 ,则 .
14. 在 中, ,则 .15. 已知定义在 上的偶函数 在 上单调递增,且 ,则不等式 的解集是.16. 过点 且平行于直线 的直线方程为.三、解答题
-
17. 已知向量 , ,函数 .(1)、求 的最大值与周期 ;(2)、求 的单调递增区间.18. 在等差数列 中, 为其前 项和 ,且(1)、求数列 的通项公式;(2)、设 ,求数列 的前 项和19. 对某电子元件进行寿命追踪调查,所得情况如下频率分布直方图.
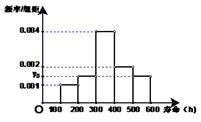 (1)、图中纵坐标 处刻度不清,根据图表所提供的数据还原 ;(2)、根据图表的数据按分层抽样,抽取 个元件,寿命为 之间的应抽取几个;(3)、从(2)中抽出的寿命落在 之间的元件中任取 个元件,求事件“恰好有一个寿命为 ,一个寿命为 ”的概率.20. 已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2.0)为其右焦点.(1)、求椭圆C的方程;(2)、是否存在平行于OA的直线L,使得直线L与椭圆C有公共点,且直线OA与L的距离等于4?若存在,求出直线L的方程;若不存在,说明理由.
(1)、图中纵坐标 处刻度不清,根据图表所提供的数据还原 ;(2)、根据图表的数据按分层抽样,抽取 个元件,寿命为 之间的应抽取几个;(3)、从(2)中抽出的寿命落在 之间的元件中任取 个元件,求事件“恰好有一个寿命为 ,一个寿命为 ”的概率.20. 已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2.0)为其右焦点.(1)、求椭圆C的方程;(2)、是否存在平行于OA的直线L,使得直线L与椭圆C有公共点,且直线OA与L的距离等于4?若存在,求出直线L的方程;若不存在,说明理由.