陕西省渭南市韩城市教学研究室2019-2020学年高三上学期数学12月月考试卷
试卷更新日期:2020-04-17 类型:月考试卷
一、单选题
-
1. 已知集合M={x|x2﹣2x﹣3≤0},N={x|y=lg(x﹣2)},则M∪N=( )A、[﹣1,+∞) B、(﹣1,+∞) C、(2,3] D、(1,3)2. 若 ,且 为第二象限角,则 ( )A、 B、 C、 D、3. 函数 的零点所在一个区间是( )A、 B、 C、 D、4. 设 , , ,则( )A、 B、 C、 D、5. 以下三个命题正确的个数有( )个.①若 ,则 或 ;②定义域为 的函数 ,函数 为奇函数是 的充分不必要条件;③若 , 且 ,则 的最小值为A、0个 B、1个 C、2个 D、3个6. 已知 是定义在R上的奇函数,当 时 (m为常数),则 的值为( )A、4 B、6 C、 D、7. 已知 有极大值和极小值,则a的取值范围为( )A、 B、 C、 或 D、 或8. 函数 的图象大致是( )A、
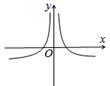 B、
B、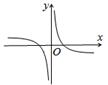 C、
C、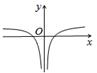 D、
D、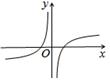 9. 已知 , 是关于 的方程 的两个实根,且 ,则 ( )A、 B、 C、 D、10. 已知命题“ ,使 ”是假命题,则实数 的取值范围是( )A、 B、 C、 D、11. 将函数 的图像上的所有点向右平移 个单位长度,得到函数 的图像,若函数 的部分图像如图所示,则函数 的解析式为( )
9. 已知 , 是关于 的方程 的两个实根,且 ,则 ( )A、 B、 C、 D、10. 已知命题“ ,使 ”是假命题,则实数 的取值范围是( )A、 B、 C、 D、11. 将函数 的图像上的所有点向右平移 个单位长度,得到函数 的图像,若函数 的部分图像如图所示,则函数 的解析式为( ) A、 B、 C、 D、12. 已知定义在 上的偶函数 的导函数为 ,函数 满足:当 时, ,且 .则不等式 的解集是( )A、 B、 C、 D、
A、 B、 C、 D、12. 已知定义在 上的偶函数 的导函数为 ,函数 满足:当 时, ,且 .则不等式 的解集是( )A、 B、 C、 D、二、填空题
-
13. 已知函数 ,则 .14. 若函数 是R上的单调函数,则实数 的取值范围是15. 已知函数 若函数 存在两个零点,则实数 的取值范围是16. 关于下列命题:①函数 在第一象限是增函数;②函数 是偶函数;③函数 的一个对称中心是 ;④函数 在闭区间 上是增函数; ⑤已知 , ,则 的最大值是 .写出所有正确的命题的题号.
三、解答题
-
17. 已知角 的顶点与原点 重合,始边与 轴的非负半轴重合,它的终边过点 .(1)、求 的值;(2)、求 的值;(3)、若角 满足 ,求 的值.18. 已知函数 .(1)、求点 处的切线方程;(2)、求函数 在 上的最值.19. 已知函数 .
(Ⅰ)求 的最小正周期及对称中心;