云南省昆明市官渡区2016-2017学年八年级下学期数学期末考试试卷

试卷更新日期：2017-09-08 类型：期末考试

进入出卷网下载

一、填空题

1. 当x时， $\sqrt{x - 3}$ 在实数范围内有意义．

查看试题解析
2. 在▱ABCD中，∠A=70°，则∠C=度．

查看试题解析
3. 正比例函数y=kx（k≠0）的图象经过点A（﹣1，5），则k= ．

查看试题解析
4. 如图，分别以Rt△ABC的三边为边长，在三角形外作三个正方形，若正方形P的面积等于89，Q的面积等于25，则正方形R的边长是．

查看试题解析
5. 如图，在平行四边形ABCD中，点E、F分别在边BC、AD上，请添加一个条件，使四边形AECF是平行四边形（只填一个即可）．

查看试题解析
6. 有两名学员小林和小明练习射击，第一轮10枪打完后两人打靶的环数如图所示，通常新手的成绩不太稳定，那么根据图中的信息，估计小林和小明两人中新手是．

查看试题解析
7. 如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB=6cm，BC=8cm，则△AEF的周长=cm．

查看试题解析
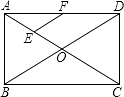8. 一次函数y₁=kx+b与y₂=x+a的图象如图所示，则不等式kx+b＜x+a的解集为．

查看试题解析

二、选择题

9. 下列二次根式中，最简二次根式是（）

A、 $\sqrt{4}$ B、 $\sqrt{8}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{11}$

查看试题解析
10. 下列计算正确的是（）

A、2 $\sqrt{3} + 4 \sqrt{2} = 6 \sqrt{5}$ B、 $\sqrt{5} - \sqrt{2} = \sqrt{3}$ C、 $\sqrt{2} (\sqrt{3} + \sqrt{5}) = \sqrt{6} + \sqrt{10}$ D、 $\sqrt{{(- 3)}^{2}}$ =﹣3

查看试题解析
11. 如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，CD是AB边上的中线，则CD的长是（）

A、20 B、10 C、5 D、 $\frac{5}{2}$

查看试题解析
12.
一次函数y=kx+b的图象如图所示，则k、b的符号（）

A、k＜0，b＞0 B、k＞0，b＞0 C、k＜0，b＜0 D、k＞0，b＜0

查看试题解析
13. 下列命题中，为真命题的是（）

A、有一组邻边相等的四边形是菱形 B、有一个角是直角的平行四边形是矩形 C、有一组对边平行的四边形是平行四边形 D、对角线互相垂直平分的四边形是正方形

查看试题解析
14. 为了调查某小区居民的用水情况，随机抽查了若干户家庭的月用水量，结果如下表：
月用水量（吨）
3
4
5
8
户数
2
3
4
1
则关于这若干户家庭的月用水量，下列说法错误的是（）

A、众数是4 B、平均数是4.6 C、调查了10户家庭的月用水量 D、中位数是4.5

查看试题解析
15. 一根蜡烛长30cm，点燃后每小时燃烧5cm，燃烧时蜡烛剩余的长度为h（cm），燃烧时间为t（小时），则下列图象能反映h与t的函数关系的是（）

A、 B、 C、 D、

查看试题解析
16. 如图，菱形ABCD的周长为40cm，对角线AC、BD相交于点O，DE⊥AB，垂足为E，DE：AB=4：5，则下列结论：①DE=8cm；②BE=4cm；③BD=4 $\sqrt{5}$ cm；④AC=8 $\sqrt{5}$ cm；⑤S_菱形ABCD=80cm，正确的有（）

A、①②④⑤ B、①②③④ C、①③④⑤ D、①②③④⑤

查看试题解析

三、解答题

17. 计算：

(1)、2 $\sqrt{12} - 6 \sqrt{\frac{1}{3}} + 3 \sqrt{48}$

(2)、 $\sqrt{27}$ ÷ $\sqrt{3}$ ﹣2 $\sqrt{\frac{1}{5}}$ × $\sqrt{10}$ + $\sqrt{8}$

(3)、 ${(\sqrt{3} + \sqrt{2})}^{2}$ ﹣（ $\sqrt{5}$ +2）（ $\sqrt{5}$ ﹣2）

查看试题解析
18. 如图所示，沿海城市B的正南方向A处有一台风中心，沿AC的方向以30km/h的速度移动，已知AC所在的方向与正北成30°的夹角，B市距台风中心最短的距离BD为120km，求台风中心从A处到达D处需要多少小时？（ $\sqrt{3} \approx 1.73$ ，结果精确到0.1）

查看试题解析
19. 已知水银体温计的读数y（℃）与水银柱的长度x（cm）之间是一次函数关系，现有一支水银体温计，其部分刻度线不清晰（如图），表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度．
水银柱的长度x（cm）
4.0
…
8.0
9.6
体温计的度数y（℃）
35.0
…
40.0
42.0

(1)、求y关于x的函数关系式（不需要写出函数自变量x的取值范围）；

(2)、用该体温计测体温时，水银柱的长度为6.0cm，求此时体温计的读数．

查看试题解析
20. 已知：如图，在▱ABCD中，E、F是对角线BD上的两点，BE=DF，求证：AE=CF．

查看试题解析
21.
某中学为了丰富学生的体育活动，决定根据学生的兴趣爱好采购一批体育用品供学生课后锻炼使用，学校随机抽取了部分同学调查他们的兴趣爱好，将收集的数据整理并绘制成下列两幅统计图，请根据图中的信息，完成下列问题：

(1)、设学校这次调查共抽取了n名学生，n= ；

(2)、请你补全条形统计图；

(3)、设该校共有学生1200名，请你估计该校有多少名学生喜欢跳绳？

查看试题解析
22. 在昆明市“创文”工作的带动下，某班学生开展了“文明在行动”的志愿者活动，准备购买一些书包送到希望学校，已知A品牌的书包每个40元，B品牌的书包每个42元，经协商：购买A品牌书包按原价的九折销售；购买B品牌的书包10个以内（包括10个）按原价销售，10个以上超出的部分按原价的八折销售．

(1)、设购买x个A品牌书包需要y₁元，求出y₁关于x的函数关系式；

(2)、购买x个B品牌书包需要y₂元，求出y₂关于x的函数关系式；

(3)、若购买书包的数量超过10个，问购买哪种品牌的书包更合算？说明理由．

查看试题解析
23. 如图，四边形ABCD中，对角线AC、BD相交于点O，AO=CO，BO=DO，且∠ABC+∠ADC=180°．

(1)、求证：四边形ABCD是矩形．

(2)、DF⊥AC，若∠ADF：∠FDC=3：2，则∠BDF的度数是多少？

查看试题解析
24. 如图，在平面直角坐标系xOy中，直线y=﹣2x+a与y轴交于点C （0，6），与x轴交于点B．

(1)、求这条直线的解析式；

(2)、直线AD与（1）中所求的直线相交于点D（﹣1，n），点A的坐标为（﹣3，0）．
①求n的值及直线AD的解析式；
②求△ABD的面积；
③点M是直线y=﹣2x+a上的一点（不与点B重合），且点M的横坐标为m，求△ABM的面积S与m之间的关系式．

查看试题解析
25. 如图，正方形ABCD中，AC是对角线，今有较大的直角三角板，一边始终经过点B，直角顶点P在射线AC上移动，另一边交DC于Q．

(1)、如图1，当点Q在DC边上时，探究PB与PQ所满足的数量关系；
小明同学探究此问题的方法是：
过P点作PE⊥DC于E点，PF⊥BC于F点，
根据正方形的性质和角平分线的性质，得出PE=PF，
再证明△PEQ≌△PFB，可得出结论，他的结论应是

(2)、如图2，当点Q落在DC的延长线上时，猜想并写出PB与PQ满足的数量关系，并证明你的猜想．

查看试题解析

水银柱的长度x（cm）	4.0	…	8.0	9.6
体温计的度数y（℃）	35.0	…	40.0	42.0

月用水量（吨）	3	4	5	8
户数	2	3	4	1