云南省红河州弥勒市2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期:2017-09-08 类型:期末考试
一、填空题
-
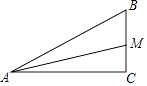
1. 已知三角形的两边长分别为3和6,那么第三边长x的取值范围是2. 如图,在△ABC中,∠C=90°,AM是∠BAC的平分线,CM=20cm,那么M到AB的距离为
 3. 因式分解:2x2﹣8= .4. 若使分式 有意义,则x的取值范围是 .5. 计算: +6 = .6. 某班学生参加环保知识竞赛,已知竞赛得分都是整数.把参赛学生的成绩整理后分为6小组,画出竞赛成绩的频数分布直方图(如图所示),根据图中的信息,可得成绩高于60分的学生占全班参赛人数的百分率是 .
3. 因式分解:2x2﹣8= .4. 若使分式 有意义,则x的取值范围是 .5. 计算: +6 = .6. 某班学生参加环保知识竞赛,已知竞赛得分都是整数.把参赛学生的成绩整理后分为6小组,画出竞赛成绩的频数分布直方图(如图所示),根据图中的信息,可得成绩高于60分的学生占全班参赛人数的百分率是 .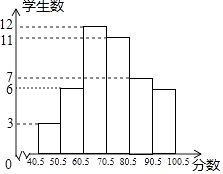
二、选择题
-
7. 若一个正多边形的一个外角是45°,则这个正多边形的边数是( )A、10 B、9 C、8 D、68. 民间剪纸是中国古老的传统民间艺术,它历史悠久,风格独特,深受国内外人士所喜爱,下列剪纸作品中,是轴对称图形的为( )A、
 B、
B、 C、
C、 D、
D、 9. 若等腰三角形中有一个角等于70°,则这个等腰三角形的顶角的度数是( )A、70° B、40° C、70°或40° D、70°或55°10. 下列计算正确的是( )A、3 ×4 =12 B、 =﹣3 C、( ﹣ )× =4 ﹣9 D、(4 ﹣3 )÷2 =2﹣11. 若下列各组数是一个三角形的三条边长,则不能组成一个直角三角形的一组数是( )A、3,4,5 B、 , , C、5,12,13 D、6,8,1012. 将函数y=﹣2x的图象向下平移3个单位,所得图象对应的函数关系式为( )A、y=﹣2(x+3) B、y=﹣2(x﹣3) C、y=﹣2x+3 D、y=﹣2x﹣313. 在一次射击训练中,甲、乙两人各射击10次,两人10次射击成绩的平均数均是9.1环,方差分别是S甲2=1.2,S乙2=1.6,则关于甲、乙两人在这次射击训练中成绩稳定的描述正确的是( )A、甲比乙稳定 B、乙比甲稳定 C、甲和乙一样稳定 D、甲、乙稳定性没法对比14.
9. 若等腰三角形中有一个角等于70°,则这个等腰三角形的顶角的度数是( )A、70° B、40° C、70°或40° D、70°或55°10. 下列计算正确的是( )A、3 ×4 =12 B、 =﹣3 C、( ﹣ )× =4 ﹣9 D、(4 ﹣3 )÷2 =2﹣11. 若下列各组数是一个三角形的三条边长,则不能组成一个直角三角形的一组数是( )A、3,4,5 B、 , , C、5,12,13 D、6,8,1012. 将函数y=﹣2x的图象向下平移3个单位,所得图象对应的函数关系式为( )A、y=﹣2(x+3) B、y=﹣2(x﹣3) C、y=﹣2x+3 D、y=﹣2x﹣313. 在一次射击训练中,甲、乙两人各射击10次,两人10次射击成绩的平均数均是9.1环,方差分别是S甲2=1.2,S乙2=1.6,则关于甲、乙两人在这次射击训练中成绩稳定的描述正确的是( )A、甲比乙稳定 B、乙比甲稳定 C、甲和乙一样稳定 D、甲、乙稳定性没法对比14.如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点O,点F、G分别是BO、CO的中点,连接AO.若AO=6cm,BC=8cm,则四边形DEFG的周长是( )
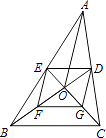 A、14cm B、18cm C、24cm D、28cm
A、14cm B、18cm C、24cm D、28cm三、解答题
-
15. 先化简,再求值:( ﹣a+2)÷ ,其中a= .16. 如图,△ABC和△CDE都是等腰直角三角形,且CA=CB,CE=CD.求证:△ACE≌△BCD.
 17. 某足球特色学校在商场购买甲、乙两种品牌的足球.已知乙种足球比甲种足球每只贵20元,该校分别花费2000元、1400元购买甲、乙两种足球,这样购得甲种足球的数量是购得乙种足球数量的2倍,求甲、乙两种足球的单价各是多少元?18. 如图所示,在四边形ABCD中,∠A=90°,AB=3,AD=4,BC=13,CD=12,求四边形ABCD的面积.
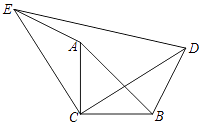
17. 某足球特色学校在商场购买甲、乙两种品牌的足球.已知乙种足球比甲种足球每只贵20元,该校分别花费2000元、1400元购买甲、乙两种足球,这样购得甲种足球的数量是购得乙种足球数量的2倍,求甲、乙两种足球的单价各是多少元?18. 如图所示,在四边形ABCD中,∠A=90°,AB=3,AD=4,BC=13,CD=12,求四边形ABCD的面积.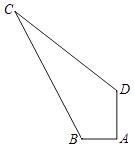 19. 如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.
19. 如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.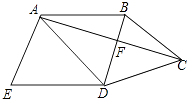 (1)、求证:四边形ABDE是平行四边形;(2)、如果DA平分∠BDE,AB=5,AD=6,求AC的长.20.
(1)、求证:四边形ABDE是平行四边形;(2)、如果DA平分∠BDE,AB=5,AD=6,求AC的长.20.在一次中学生田径运动会上,根据参加男子跳高初赛运动员的成绩(单位:m),绘制出如下所示的条形统计图和扇形统计图,请根据统计图相关信息,解答下列问题:
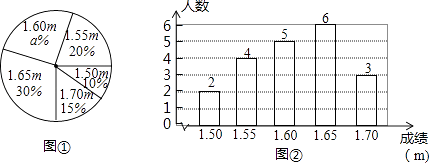 (1)、求扇形统计图中a值;(2)、求男子跳高初赛成绩的平均数、众数和中位数.21. 已知正比例函数y1=﹣2x的图象如图所示.
(1)、求扇形统计图中a值;(2)、求男子跳高初赛成绩的平均数、众数和中位数.21. 已知正比例函数y1=﹣2x的图象如图所示.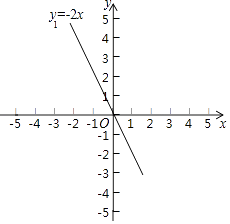 (1)、在如图所示的平面直角坐标系中,画出一次函数y2=2x﹣4的图象;(2)、求正比例函数y=﹣2x和一次函数y=2x﹣4的交点坐标;(3)、若y2<y1 , 则由(2)直接写出自变量x的取值范围.22.
(1)、在如图所示的平面直角坐标系中,画出一次函数y2=2x﹣4的图象;(2)、求正比例函数y=﹣2x和一次函数y=2x﹣4的交点坐标;(3)、若y2<y1 , 则由(2)直接写出自变量x的取值范围.22.如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=30cm.点P从点A出发,以1cm/s的速度向点D移动,点Q从点C出发,以3cm/s的速度向点B运动,点P和点Q分别从点A和点C同时出发,移动时间为ts.规定若其中一个动点先到达端点(终点)时,另一个动点也随之停止运动.
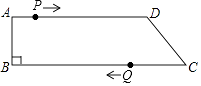 (1)、求时间t的取值范围;(2)、当四边形ABQP为矩形时,求时间t的值;
(1)、求时间t的取值范围;(2)、当四边形ABQP为矩形时,求时间t的值;
(3)、是否存在时间t的值,使得△APQ的面积是△ABC的面积的一半?若存在,请求出t的值,若不存在,说明理由.23. 水果市场中的甲、乙两家商店中都批发同一种水果,批发水果x千克时,在甲、乙两家商店的批发价分别为y1元和y2元,已知y1和y2关于x的函数图象分别为如图所示的折线OAB和射线OC.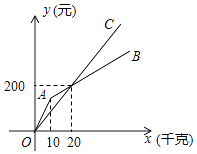 (1)、请求出y2与自变量x的函数解析式,并写出自变量x的取值范围;(2)、当乙商店的批发价比甲商店的批发价便宜时,根据函数图象直接写出自变量x的取值范围;(3)、如果批发30千克水果时,在甲店批发比在乙店批发便宜50元,求射线AB的函数解析式并写出自变量x的取值范围.
(1)、请求出y2与自变量x的函数解析式,并写出自变量x的取值范围;(2)、当乙商店的批发价比甲商店的批发价便宜时,根据函数图象直接写出自变量x的取值范围;(3)、如果批发30千克水果时,在甲店批发比在乙店批发便宜50元,求射线AB的函数解析式并写出自变量x的取值范围.