天津市部分区2016-2017学年八年级下学期数学期末考试试卷

试卷更新日期：2017-09-08 类型：期末考试

进入出卷网下载

一、选择题

1. 如果 $\sqrt{a + 2}$ 有意义，那么（）

A、a≥﹣2 B、a≤2 C、a≥2 D、a≤﹣2

查看试题解析
2. 下列二次根式，不能与 $\sqrt{2}$ 合并的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{8}$ C、 $\sqrt{12}$ D、﹣ $\sqrt{18}$

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{3}$ + $\sqrt{5}$ = $\sqrt{8}$ B、 $\sqrt{8}$ ﹣ $\sqrt{3}$ = $\sqrt{8 - 3}$ C、 $\sqrt{3 \frac{2}{3}}$ =3 $\sqrt{\frac{2}{3}}$ D、 $\frac{\sqrt{2}}{\sqrt{5}}$ = $\frac{\sqrt{10}}{5}$

查看试题解析
4. 如果下列各组数是三角形的三边长，那么不能组成直角三角形的一组数是（）

A、6，8，10 B、4，5，6 C、 $\frac{5}{4}$ ，1， $\frac{3}{4}$ D、 $\sqrt{41}$ ，4，5

查看试题解析
5.
如图，在平面直角坐标系中，有两点坐标分别为（2，0）和（0，3），则这两点之间的距离是（）

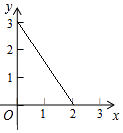A、 $\sqrt{13}$ B、 $\sqrt{5}$ C、13 D、5

查看试题解析
6. 某市测得一周PM2.5的日均值（单位：）如下：50，40，75，50，37，50，40，这组数据的中位数和众数分别是（）

A、50和50 B、50和40 C、40和50 D、40和40

查看试题解析
7. 若平行四边形中两个内角的度数比为1：2，则其中较小的内角是（）

A、90° B、60° C、120° D、45°

查看试题解析
8. 下列说法不正确的是（）

A、对角线互相垂直的矩形一定是正方形 B、对角线相等的菱形一定是正方形 C、对角线互相垂直且相等的平行四边形一定是正方形 D、顺次连接任意对角线相等的四边形的各边中点所得的四边形一定是正方形

查看试题解析
9. 如图，菱形ABCD的边长为20，∠DAB=60，对角线为AC和BD，那么菱形的面积为（）

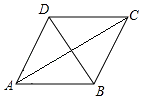A、50 $\sqrt{3}$ B、100 $\sqrt{3}$ C、200 $\sqrt{3}$ D、400 $\sqrt{3}$

查看试题解析
10. 下列变量之间关系中，一个变量是另一个变量的正比例函数的是（）

A、正方形的面积S随着边长x的变化而变化 B、正方形的周长C随着边长x的变化而变化 C、水箱有水10L，以0.5L/min的流量往外放水，水箱中的剩水量V（L）随着放水时间t（min）的变化而变化 D、面积为20的三角形的一边a随着这边上的高h的变化而变化

查看试题解析
11. 一次函数y=kx+b中，y随x的增大而减小，b＜0，则这个函数的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
12. 某书定价8元，如果一次购买10本以上，超过10本部分打八折，那么付款金额y与购书数量x之间的函数关系如何，同学们对此展开了讨论：
⑴小明说：y与x之间的函数关系为y=6.4x+16
⑵小刚说：y与x之间的函数关系为y=8x
⑶小聪说：y与x之间的函数关系在0≤x≤10时，y=8x；在x＞10时，y=6.4x+16
⑷小斌说：我认为用下面的列表法也能表示它们之间的关系
购买量/本
1
2
3
4
…
9
10
11
12
…
付款金额/元
8
16
24
32
…
72
80
86.4
92.8
…
⑸小志补充说：如图所示的图象也能表示它们之间的关系．
其中，表示函数关系正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 计算：（2 $\sqrt{7}$ ）²= ．

查看试题解析
14. 在△ABC中，∠C=90°，AC=6，BC=8，则高CD的长为．

查看试题解析
15. 已知点（﹣2，y₁），（3，y₂）都在直线y=kx﹣1上，若y₁＜y₂ ，则k0．（填＞，＜或=）

查看试题解析
16. 已知矩形ABCD的对角线AC，BD相交于点O，∠AOB=60°，AB=4，则矩形对角线的长是．

查看试题解析
17. 函数y=kx与y=6﹣x的图象如图所示，则k= ．

查看试题解析
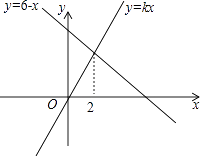18. 如图，在梯形ABCD中，AD∥BC，AD=6，BC=16，E是BC的中点．点P以每秒1个单位长度的速度从点A出发，沿AD向点D运动；点Q同时以每秒2个单位长度的速度从点C出发，沿CB向点B运动．点P停止运动时，点Q也随之停止运动．当运动时间秒时，以点P，Q，E，D为顶点的四边形是平行四边形．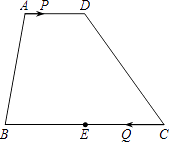

查看试题解析

三、解答题

19. 计算：
（Ⅰ） $\sqrt{18}$ × $\sqrt{20}$ × $\sqrt{75}$
（Ⅱ）（ $\sqrt{12}$ + $\sqrt{20}$ ）+（ $\sqrt{3}$ ﹣ $\sqrt{5}$ ）

查看试题解析
20. 为了考察甲、乙两种小麦的长势，分别从中抽取5株麦苗，测得苗高（单位：cm）如下：
甲：6、8、9、9、8；
乙：10、7、7、7、9．
（Ⅰ）分别计算两种小麦的平均苗高；
（Ⅱ）哪种小麦的长势比较整齐？为什么？

查看试题解析
21. 如图，在矩形ABCD中，AB=8，AD=4，点E，F分别在边CD，AB上，若四边形AFCE是菱形，求菱形AFCE的周长．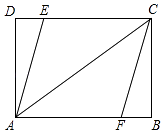

查看试题解析
22. 直线a：y=x+2和直线b：y=﹣x+4相交于点A，分别与x轴相交于点B和点C，与y轴相交于点D和点E．

(1)、求△ABC的面积；

(2)、求四边形ADOC的面积．

查看试题解析
23.
某商场服装部为了解服装的销售情况，统计了每位营业员在某月的销售额（单位：万元），并根据统计的这组数据，绘制出如下的统计图①和图②．请根据相关信息，解答下列问题．

(1)、该商场服装部营业员的人数为，图①中m的值为 .

(2)、求统计的这组销售额额数据的平均数、众数和中位数．

查看试题解析
24. 如图（1），正方形ABCD的对角线AC，BD相交于点O，E是AC上一点，连结EB，过点A作AM⊥BE，垂足为M，AM与BD相交于点F．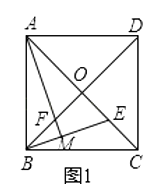

(1)、求证：OE=OF；

(2)、如图（2）若点E在AC的延长线上，AM⊥BE于点M，AM交DB的延长线于点F，其他条件不变，结论“OE=OF”还成立吗？如果成立，请给出证明；如果不成立，请说明理由．

查看试题解析
25. 为保障我人民海军的海上生活，现需通过A港、B港分别运送200t和300t生活物资．已知该物资在甲仓库存有240t，乙仓库存有260t，若从甲、乙两仓运送物资到港口A的费用分别为20元/t、15元/t；从甲、乙两仓运送物资到港口B的费用分别为25元/t、24元/t．

(1)、若设从甲仓库运往A港x吨，试填写表格．
表一：
港口
从甲仓库运（吨）
从乙仓库运（吨）
A港
x
B港
表二：
港口
从甲仓库运到港口费用（元）
从乙仓库运到港口费用（元）
A港
20x
B港

(2)、给出能完成此次运输任务的总费用最少的调运方案，并说明理由．

查看试题解析

购买量/本	1	2	3	4	…	9	10	11	12	…
付款金额/元	8	16	24	32	…	72	80	86.4	92.8	…

港口	从甲仓库运（吨）	从乙仓库运（吨）
A港	x
B港

港口	从甲仓库运到港口费用（元）	从乙仓库运到港口费用（元）
A港	20x
B港