山西省运城市盐湖区2016-2017学年八年级下学期数学期末考试试卷

试卷更新日期：2017-09-08 类型：期末考试

进入出卷网下载

一、选择题

1. 正十二边形的每一个内角的度数为（）

A、120° B、135° C、1080° D、150°

查看试题解析
2. 下列多项式中，能用完全平方式分解的是（）

A、x²﹣x+1 B、1﹣2xy+x²y² C、 $a^{2} + a + \frac{1}{2}$ D、﹣a²+b²﹣2ab

查看试题解析
3. 若不等式组 ${\begin{matrix} 2 x - 1 < 3 \\ x < a \end{matrix}$ 的解集是x＜2，则a的取值范围是（）

A、a＜2 B、a≤2 C、a≥2 D、无法确定

查看试题解析
4. 已知，Rt△ABC中，∠C=90°，AD平分∠BAC交BC于D，若BC=32，且BD：CD=9：7，则D到AB的距离为（）

A、18 B、16 C、14 D、12

查看试题解析
5. 若将点A（1，3）向左平移2个单位，再向下平移4个单位得到点B，则点B的坐标为（）

A、（﹣2，﹣1） B、（﹣1，0） C、（﹣1，﹣1） D、（﹣2，0）

查看试题解析
6. 若关于x的方程 $\frac{x + m}{x - 3}$ + $\frac{3 m}{3 - x}$ =3的解为正数，则m的取值范围是（）

A、m＜ $\frac{9}{2}$ B、m＜ $\frac{9}{2}$ 且m≠ $\frac{3}{2}$ C、m＞﹣ $\frac{9}{4}$ D、m＞﹣ $\frac{9}{4}$ 且m≠﹣ $\frac{3}{4}$

查看试题解析
7. 一次函数y₁=kx+b与y₂=x+a的图象如图，则下列结论①k＜0；②a＞0；③当x＜3时，y₁＜y₂中，正确的个数是（）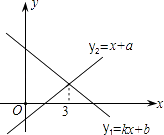

A、0 B、1 C、2 D、3

查看试题解析
8. 为抢修因连日暴雨而损坏的一段长120米的高速公路，施工队每天比原计划多修5米，结果提前4天完成了任务．问原计划每天修多少米？设原计划每天修x米，所列方程正确的是（）

A、 $\frac{120}{x + 5} - \frac{120}{x} = 4$ B、 $\frac{120}{x} - \frac{120}{x - 5} = 4$ C、 $\frac{120}{x - 5} - \frac{120}{x} = 4$ D、 $\frac{120}{x} - \frac{120}{x + 5} = 4$

查看试题解析
9. 已知A，B，C三点的坐标分别为（3，3），（8，3），（4，6），若以A，B，C，D四点为顶点的四边形是平行四边形，则D点的坐标不可能是（）

A、（﹣1，6） B、（9，6） C、（7，0） D、（0，﹣6）

查看试题解析
10. 如图，D为△ABC内一点，CD平分∠ACB，BE⊥CD，垂足为D，交AC于点E，∠A=∠ABE．若AC=5，BC=3，则BD的长为（）

A、2.5 B、1.5 C、2 D、1

查看试题解析

二、填空题

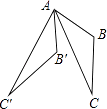
11. 分解因式：a³﹣a= ．

查看试题解析
12. 若不等式（a+1）x＞a+1的解集是x＜1，则a的取值范围是．

查看试题解析
13. 如图所示，△ABC中，∠BAC=33°，将△ABC绕点A按顺时针方向旋转50°，对应得到△AB′C′，则∠B′AC的度数为．

查看试题解析
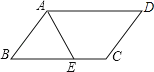
14.
在平行四边形ABCD中，∠BAD的平分线AE交BC于点E，且BE=3，若平行四边形ABCD的周长是16，则EC等于．

查看试题解析
15. 如图是一张长方形纸片ABCD，已知AB=8，AD=7，E为AB上一点，AE=5，现要剪下一张等腰三角形纸片（△AEP），使点P落在长方形ABCD的某一条边上，则等腰三角形AEP的底边长是．

查看试题解析

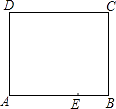
三、解答题

16. 因式分解：2x²﹣4x+2．

查看试题解析
17. 先化简，再求值．
在﹣2，﹣1，0，1，2中选一个你认为合适的数作为a的值，求（ $\frac{2 - 2 a}{a + 1}$ +a﹣1）÷ $\frac{a^{2} - a}{a + 1}$ 的值．

查看试题解析
18. 解不等式组 ${\begin{matrix} 3 x + 1 \leq 2 (x + 1) \\ - x < 5 x + 12 \end{matrix}$ ，并写出它的整数解．

查看试题解析
19. 解分式方程： $\frac{1 - x}{x - 2} + 2 = \frac{1}{2 - x}$ ．

查看试题解析
20. 阅读下面的题目及分析过程，并按要求进行证明．
已知：如图，E是BC的中点，点A在DE上，且∠BAE=∠CDE．
求证：AB=CD．
分析：证明两条线段相等，常用的一般方法是应用全等三角形或等腰三角形的判定和性质，观察本题中要证明的两条线段，它们不在同一个三角形中，且它们分别所在的两个三角形也不全等．因此，要证AB=CD，必须添加适当的辅助线，构造全等三角形或等腰三角形．
现给出如下三种添加辅助线的方法，请任意选择其中一种，对原题进行证明．

查看试题解析
21. 某工程队由甲乙两队组成，承包我市河东东街改造工程，规定若干天完成，已知甲单独完成这项工程所需时间比规定时间多32天，乙队单独完成这项工程所需时间比规定时间多12天，如果甲乙两队先合作20天，剩下的甲单独做，则延误两天完成，那么规定时间是多少天？

查看试题解析
22.
如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）

(1)、请画出将△ABC向左平移4个单位长度后得到的图形△A₁B₁C₁；

(2)、请画出△ABC关于原点O成中心对称的图形△A₂B₂C₂；

(3)、在x轴上找一点P，使PA+PB的值最小，请直接写出点P的坐标．

查看试题解析
23. 已知E为平行四边形ABCD中AB边上一点，且BE=AB，连接DE交BC于F，交AC于G．

(1)、求证：△BEF≌△CDF；

(2)、试探究OF与AB有什么位置关系和数量关系，并说明理由．

查看试题解析