北京市通州区2020年中考数学三模考试试卷

试卷更新日期：2020-04-16 类型：中考模拟

进入出卷网下载

一、选择题（共8小题）

1. 下列几何体中，侧面展开图是矩形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 若实数a，b，c，d在数轴上的对应点的位置如图所示，则正确结论是（　　）

A、|a|＞4 B、b+d＜0 C、ac＞0 D、a﹣c＞0

查看试题解析
3. 若二元一次方程组 ${\begin{cases} x + 2 y = 2 \\ 2 x - y = 4 \end{cases}$ 的解为 ${\begin{cases} x = a \\ y = b \end{cases}$ 则a+b的值为（　　）

A、0 B、1 C、2 D、4

查看试题解析
4. 2019年4月17日，国家统计局公布2019年一季度中国经济数据．初步核算，一季度国内生产总值213433亿元，按可比价格计算，同比增长6.4%．数据213433亿用科学记数法表示应为（　　）

A、2.13433×10¹³ B、0.213433×10¹⁴ C、213.433×10¹² D、2.13433×10¹⁴

查看试题解析
5. 一个多边形的内角和比它的外角和还大180°，这个多边形的边数为（　　）

A、8 B、7 C、6 D、5

查看试题解析
6. 如果x²+x﹣3＝0，那么代数式（ $\frac{x}{x - 1}$ ﹣1）÷ $\frac{x^{3} - 3}{x^{2} - 2 x + 1}$ 的值为（　　）

A、﹣ $\frac{1}{3}$ B、0 C、 $\frac{1}{3}$ D、3

查看试题解析
7. 四位同学在研究二次函数y＝ax²+bx+3（a≠0）时，甲同学发现函数图象的对称轴是直线x＝1；乙同学发现3是一元二次方程ax²+bx+3＝0（a≠0）的一个根；丙同学发现函数的最大值为4；丁同学发现当x＝2时，y＝5，已知这四位同学中只有一位同学发现的结论是不正确，则该同学是（　　）

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 如图是2019北京世园会的部分场馆展示区的分布示意图．当表示国际馆A馆的点的坐标为（325，0），表示九州花境的点的坐标为（﹣65，460）时，则建立的平面直角坐标系，x轴最有可能的位置是（　　）

A、表示中国馆和世艺花舞的两点所在的直线 B、表示中国馆和中华园艺展示区的两点所在的直线 C、表示中国馆和九州花境的两点所在的直线’ D、表示百松云屏和中华园艺展示区的两点所在的直线

查看试题解析

二、填空题（共8小题）

9. 在如图所示的正方形网格中，∠1∠2．（填“＞”，“＝”，“＜”）

查看试题解析
10. 若 $\frac{1}{2 - x}$ 在实数范围内有意义，则实数x的取值范围是．

查看试题解析
11. 已知二次函数y＝ax²+bx﹣2（a≠0）的图象的对称轴在y轴的左侧，请写出满足条件的一组a，b的值，这组值可以是a＝， b＝．

查看试题解析
12. 如图，在⊙O中，直径AB与弦CD的交点为E，AC∥OD．若∠BEC＝72°，则∠B＝°．

查看试题解析
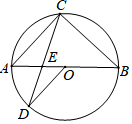13. 如图，平行四边形ABCD的对角线AC，BD的交点为O，AC⊥AB，CD边的中点为E．若OA＝2，AB＝3，则OE＝．

查看试题解析

14. 为了了解学生每月的零用钱情况，从甲、乙、丙三个学校各随机抽取200名学生，调查了他们的零用钱情况（单位：元）具体情况如下：

学校频数零用钱	100≤x＜200	200≤x＜300	300≤x＜400	400≤x＜500	500以上	合计
甲	5	35	150	8	2	200
乙	16	54	68	52	10	200
丙	0	10	40	70	80	200

在调查过程中，从（填“甲”，“乙”或“丙”）校随机抽取学生，抽到的学生“零用钱不低于300元”的可能性最大．

查看试题解析

15. 甲地有42吨货物要运到乙地，有大、小两种货车可供选择，具体收费情况如表：

类型

载重量（吨）

运费（元/车）

大货车

8

450

小货车

5

300

运完这批货物最少要支付运费元．

查看试题解析
16. 某市多措并举，加强空气质量治理，空气质量达标天数显著增加，重污染天数逐年减少，越来越多的蓝天出现在人们的生活中．下图是该市4月1日至15日的空气质量指数趋势图，空气质量指数小于100表示空气质量为优良．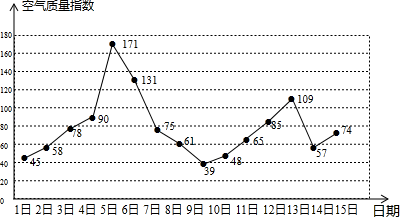

由上图信息，在该市4月1日至15日空气质量为优良的时间里，从第日开始，连续三天空气质量指数的方差最小．

查看试题解析

三、解答题（共12小题）

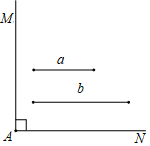
17. 已知：如图，∠MAN＝90°，线段a和线段b
求作：矩形ABCD，使得矩形ABCD的两条边长分别等于线段a和线段b．

下面是小东设计的尺规作图过程．

作法：如图，

①以点A为圆心，b为半径作弧，交AN于点B；

②以点A为圆心，a为半径作弧，交AM于点D；

③分别以点B、点D为圆心，a、b长为半径作弧，两弧交于∠MAN内部的点C；

④分别连接BC，DC．

所以四边形ABCD就是所求作的矩形．

根据小东设计的尺规作图过程，

(1)、使用直尺和圆规，补全图形；（保留作图痕迹）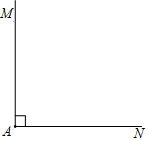

(2)、完成下面的证明．
证明：

∵AB＝；AD＝；

∴四边形ABCD是平行四边形．

∵∠MAN＝90°；

∴四边形ABCD是矩形（填依据）．

查看试题解析
18. 计算：3tan30°﹣（﹣ $\frac{1}{3}$ ）^﹣1+2019⁰+| $\sqrt{3}$ ﹣2|．

查看试题解析
19. 解不等式组 ${\begin{cases} 4 (x + 2) < 6 x + 9 \\ \frac{x + 11}{3} \leq 5 - x \end{cases}$ ，并写出它的所有非负整数解．

查看试题解析
20. 关于x的一元二次方程x²+2mx+m²+m﹣2＝0有两个实数根．

(1)、求m的取值范围；

(2)、若m为正整数，且方程的根都是负整数，求m的值．

查看试题解析
21. 如图，在▱ABCD中，AE⊥BC于点E，过点D作DF∥AE，交BC的延长线于点F，连接AF．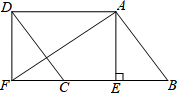

(1)、求证：四边形AEFD是矩形；

(2)、若AD＝8，tanB＝ $\frac{4}{3}$ ，CF＝ $\frac{9}{2}$ ，求AF的长．

查看试题解析
22. 如图，在Rt△ABC中，∠C＝90°，AE是△ABC的角平分线．AE的垂直平分线交AB于点O，以点O为圆心，OA为半径作⊙O，交AB于点F．

(1)、求证：BC是⊙O的切线；

(2)、若AC＝2，tanB＝ $\frac{1}{2}$ ，求⊙O的半径r的值．

查看试题解析
23. 如图，在平面直角坐标系xOy中，B（3，﹣3），C（5，0），以OC，CB为边作平行四边形OABC，函数y＝ $\frac{k}{x}$ （x＜0）的图象经过点A．

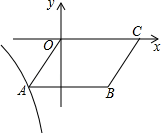(1)、求k的值；

(2)、若过点A的直线l平行于直线OB，且交函数y＝ $\frac{k}{x}$ （x＜0）的图象于点D．
①求直线l的表达式；

②定义：横、纵坐标都是整数的点叫做整点．记函数y＝ $\frac{k}{x}$ （x＜0）的图象在点A，D之间的部分与线段AD围成的区域（含边界）为W．结合函数图象，直接写出区域W内（含边界）的整点个数．

查看试题解析

24. 如图，已知线段AB＝6cm，过点B做射线BF且满足∠ABF＝40°，点C为线段AB中点，点P为射线BF上的动点，连接PA，过点B作PA的平行线交射线PC于点D，设PB的长度为xcm，PD的长度为y₁cm，BD的长度为y₂cm．（当点P与点B重合时，y₁与y₂的值均为6cm）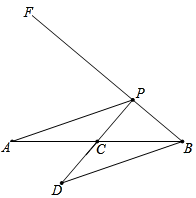

小腾根据学习函数的经验，分别对函数y₁ ， y₂随自变量x的变化而变化的规律进行了探究．

下面是小腾的探究过程，请补充完整：

(1)、按照下表中自变量x （0≤x≤6）的值进行取点、画图、测量，分别得到了y₁ ， y₂与x的几组对应值：

x/cm	0	1	2	3	4	5	6
y₁/cm	6.0	4.7	3.9	4.1	5.1	6.6	8.4
y₂/cm	6.0	5.3	4.7	4.2		3.9	4.1

（说明：补全表格时相关数值保留一位小数）

(2)、在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x，y₁），（x，y₂），并画出y₁ ， y₂的图象；

(3)、结合函数图象解决问题：当△PDB为等腰三角形时，则BP的长度约为cm；

(4)、当x＞6时，是否存在x的值使得△PDB为等腰三角形（填“是”或者“否”）．

查看试题解析

25. 为了调查A、B两个区的初三学生体育测试成绩，从两个区各随机抽取了1000名学生的成绩（满分：40分，个人成绩四舍五入向上取整数）

A区抽样学生体育测试成绩的平均分、中位数、众数如下：

平均分

中位数

众数

37

36

37

B区抽样学生体育测试成绩的分布如下：

成绩

28≤x＜31

31≤x＜34

34≤x＜37

37≤x＜40

40（满分）

人数

60

80

140

m

220

请根据以上信息回答下列问题

(1)、m＝；

(2)、在两区抽样的学生中，体育测试成绩为37分的学生，在（填“A”或“B”）区被抽样学生中排名更靠前，理由是；

(3)、如果B区有10000名学生参加此次体育测试，估计成绩不低于34分的人数．

查看试题解析
26. 在平面直角坐标系xOy中，抛物线y＝ax²﹣4ax+4（a≠0）与y轴交于点A．

(1)、求点A的坐标和抛物线的对称轴；

(2)、过点B（0，3）作y轴的垂线l，若抛物线y＝ax²﹣4ax+4（a≠0）与直线l有两个交点，设其中靠近y轴的交点的横坐标为m，且|m|＜1，结合函数的图象，求a的取值范围．

查看试题解析
27. 如图，在△ABC中，AB＝AC＝5，BC＝6，点M在△ABC内，AM平分∠BAC．点E与点M在AC所在直线的两侧，AE⊥AB，AE＝BC，点N在AC边上，CN＝AM，连接ME，BN．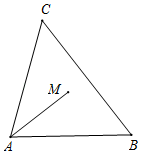

(1)、补全图形；

(2)、求ME：BN的值；

(3)、问：点M在何处时BM+BN取得最小值？确定此时点M的位置，并求此时BM+BN的最小值．

查看试题解析
28. 在平面直角坐标系xOy中，点P，Q（两点可以重合）在x轴上，点P的横坐标为m，点Q的横坐标为n，若平面内的点M的坐标为（n，|m﹣n|），则称点M为P，Q的跟随点．

(1)、若m＝0，
①当n＝3时，P，Q的跟随点的坐标为多少；

②写出P，Q的跟随点的坐标；（用含n的式子表示）；

③记函数y＝kx﹣1（﹣1≤x≤1，k≠0）的图象为图形G，若图形G上不存在P，Q的跟随点，求k的取值范围；

(2)、⊙A的圆心为A（0，2），半径为1，若⊙A上存在P，Q的跟随点，直接写出m的取值范围．

查看试题解析

类型	载重量（吨）	运费（元/车）
大货车	8	450
小货车	5	300

成绩	28≤x＜31	31≤x＜34	34≤x＜37	37≤x＜40	40（满分）
人数	60	80	140	m	220

平均分	中位数	众数
37	36	37