北京市顺义区2019年中考数学一模考试试卷

试卷更新日期：2020-04-16 类型：中考模拟

进入出卷网下载

一、选择题（本题共16分，每小题2分）第1-8题均有四个选。正确选项只有一个．

1. 下面四个美术字中可以看作轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 有理数a，b在数轴上的位置如图所示，以下说法正确是（　　）

A、a+b＝0 B、a﹣b＞0 C、ab＞0 D、|b|＜|a|

查看试题解析
3. 如图所示，该几何体的主视图是（　　）

A、 B、 C、 D、

查看试题解析
4. 一个多边形的内角和是720°，这个多边形是（）

A、五边形 B、六边形 C、七边形 D、八边形

查看试题解析
5. 已知点M（1﹣2m，m﹣1）在第二象限，则m的取值范围是（　　）

A、m＞1 B、 $m < \frac{1}{2}$ C、 $\frac{1}{2} < m < 1$ D、 $- \frac{1}{2} < m < 1$

查看试题解析
6. 如图，A处在B处的北偏东45°方向，A处在C处的北南偏西15°方向，则∠BAC等于（　　）

A、30° B、45° C、50° D、60°

查看试题解析
7. 如图，随机闭合开关S₁ ， S₂ ， S₃中的两个，则灯泡发光的概率为（　　）

A、 $\frac{3}{4}$ B、 $\frac{2}{3}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
8. 如图，点A，C，E，F在直线l上，且AC＝2，EF＝1，四边形ABCD，EFGH，EFNM均为正方形，将正方形ABCD沿直线l向右平移，若起始位置为点C与点E重合，终止位置为点A与点F重合．设点C平移的距离为x，正方形ABCD的边位于矩形MNGH内部的长度为y，则y与x的函数图象大致为（　　）

A、 B、 C、 D、

查看试题解析

二、填空题（本题共16分，每小题2分）

9. 分解因式：a²b﹣4ab²+4b³= ．

查看试题解析
10. 已知：m、n为两个连续的整数，且m＜ $\sqrt{11}$ ＜n，则m+n= ．

查看试题解析
11. 已知|x﹣y+3|+ $\sqrt{2 x + y}$ ＝0，则x•y的值为．

查看试题解析
12. 如图，等边三角形ABC内接于⊙O，点D在⊙O上，∠ABD＝25°，则∠BAD＝°．

查看试题解析
13. 如图是北京市2019年3月1日至20日的空气质量指数趋势图，空气质量指数小于100表示空气质量优良．那么在这20天中空气质量优良天数比例是．

查看试题解析
14. 如图，DE为△ABC的中位线，点F在DE上，且∠AFB＝90°，若AB＝6，BC＝8，则EF的长为．

查看试题解析
15. 《孙子算经》是中国古代重要的数学著作，成书于约一千五百年前，其中有首歌谣：“今有竿不知其长，量得影长一丈五尺，立一标杆，长一尺五寸，影长五寸，问竿长几何？”意思就是：有一根竹竿不知道有多长，量出它在太阳下的影子长一丈五尺，同时立一根一尺五寸的小标杆（如图所示），它的影长五寸（提示：1丈＝10尺，1尺＝10寸），则竹竿的长为．

查看试题解析
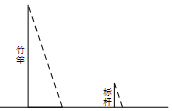16. 利用二维码可以进行身份识别．某校建立了一个身份识别系统，图1是某个学生的识别图案，黑色小正方形表示1，白色小正方形表示0，将第一行数字从左到右依次记为a，b，c，d，那么可以转换为该生所在班级序号，其序号为a×2³+b×2²+c×2¹+d×2⁰ ．如图1中的第一行数字从左到右依次为0，1，0，1，序号即为0×2³+1×2²+0×2¹+1×2⁰＝5，表示该生为5班学生．若想在图2中表示4班学生的识别图案，请问应该把标号为①、②、③、④的正方形中的（只填序号）涂成黑色．

查看试题解析

三、解答题（本题共68分，第17-22题，每小题5分，第23-26题，每小题5分，第27、28题，每小题5分）解答应写出文字说明，演算步骤或证明过程．

17. 计算： $\sqrt{12}$ ﹣3tan30°﹣（1﹣π）⁰+|1﹣ $\sqrt{3}$ |．

查看试题解析
18. 已知x²+3x﹣3＝0，求代数式 $(1 - \frac{3}{x}) \div \frac{x - 3}{x + 3} - \frac{x + 6}{x + 3}$ 的值．

查看试题解析
19. 下面是小明同学设计的“过直线外一点作这条直线的垂线”的尺规作图过程．
已知：直线l及直线l外一点P．

求作：直线PQ，使得PQ⊥l．

作法：如图，

①在直线l上取一点A，以点P为圆心，PA长为半径画弧，与直线l交于另一点B；

②分别以A，B为圆心，PA长为半径在直线l下方画弧，两弧交于点Q；

③作直线PQ．

所以直线PQ为所求作的直线．

根据小明设计的尺规作图过程，

(1)、使用直尺和圆规，补全图形；（保留作图痕迹）

(2)、完成下面的证明．
证明：连接PA，PB，QA，QB．

∵PA＝PB＝QA＝QB，

∴四边形APBQ是菱形（填推理的依据）．

∴PQ⊥AB（填推理的依据）．

即PQ⊥l．

查看试题解析
20. 关于x的一元二次方程x²﹣4x+m﹣1＝0有两个不相等的实数根．

(1)、求m的取值范围；

(2)、若m为正整数，且该方程的根都是整数，求m的值．

查看试题解析
21. 已知：如图，四边形ABCD是矩形，∠ECD＝∠DBA，∠CED＝90°，AF⊥BD于点F．

(1)、求证：四边形BCEF是平行四边形；

(2)、若AB＝4，AD＝3，求EC的长．

查看试题解析
22. 已知：如图，AB是⊙O的直径，点C是⊙O上一点，点P在AB的延长线上，且∠A＝∠P＝30．

(1)、求证：PC是⊙O的切线；

(2)、连接BC，若AB＝4，求△PBC的面积．

查看试题解析
23. 在平面直角坐标系xOy中，直线y＝2x﹣6与双曲线y= $\frac{k}{x}$ （k≠0）的一个交点为A（m，2），与x轴交于点B，与y轴交于点C．

(1)、求点B的坐标及k的值；

(2)、若点P在x轴上，且△APC的面积为16，求点P的坐标．

查看试题解析

24. 为了传承中华优秀传统文化，某校学生会组织了一次全校1200名学生参加的“汉字听写”大赛，并设成绩优胜奖．

赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，随机抽取了其中100名学生的成绩作为样本进行整理，得到下列不完整的统计图表：

成绩x/分	频数	频率
50≤x＜60	10	0.10
60≤x＜70	25	0.25
70≤x＜80	30	b
80≤x＜90	a	0.20
90≤x≤100	15	0.15

成绩在70≤x＜80这一组的是：

70 70 71 71 71 72 72 73 73 73 73 75 75 75 75 76 76 76 76 76 76 76 76 77 77 78 78 78 79 79

请根据所给信息，解答下列问题：

(1)、a＝， b＝；

(2)、请补全频数分布直方图；

(3)、这次比赛成绩的中位数是；

(4)、若这次比赛成绩在78分以上（含78分）的学生获得优胜奖，则该校参加这次比赛的1200名学生中获优胜奖的约有多少人？

查看试题解析

25. 有这样一个问题：探究函数y＝

\frac{1}{x - 2}

+x的图象与性质．

小亮根据学习函数的经验，对函数y＝ $\frac{1}{x - 2}$ +x的图象与性质进行了探究．

下面是小亮的探究过程，请补充完整：

(1)、函数y＝

\frac{1}{x - 2}

+x中自变量x的取值范围是；

(2)、下表是y与x的几组对应值．

…

﹣2

﹣1

$\frac{3}{2}$

$\frac{7}{4}$

$\frac{9}{4}$

$\frac{5}{2}$

…

﹣ $\frac{9}{4}$

﹣ $\frac{4}{3}$

﹣ $\frac{1}{2}$

﹣ $\frac{9}{4}$

$\frac{25}{4}$

$\frac{9}{2}$

$\frac{16}{3}$

$\frac{25}{4}$

…

求m的值；

(3)、在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；

(4)、根据画出的函数图象，发现下列特征：

①该函数的图象是中心对称图形，对称中心的坐标是；

②该函数的图象与过点（2，0）且平行于y轴的直线越来越靠近而永不相交，该函数的图象还与直线越来越靠近而永不相交．

查看试题解析

26. 在平面直角坐标系xOy中，抛物线y＝mx²+（m﹣3）x﹣3（m＞0）与x轴交于A、B两点（点A在点B左侧），与y轴交于点C，AB＝4，点D为抛物线的顶点．

(1)、求点A和顶点D的坐标；

(2)、将点D向左平移4个单位长度，得到点E，求直线BE的表达式；

(3)、若抛物线y＝ax²﹣6与线段DE恰有一个公共点，结合函数图象，求a的取值范围．

查看试题解析
27. 已知：如图，在△ABC中，AB＞AC，∠B＝45°，点D是BC边上一点，且AD＝AC，过点C作CF⊥AD于点E，与AB交于点F．

(1)、若∠CAD＝α，求∠BCF的大小（用含α的式子表示）；

(2)、求证：AC＝FC；

(3)、用等式直接表示线段BF与DC的数量关系．

查看试题解析
28. 在平面直角坐标系xOy中，A、B为平面内不重合的两个点，若Q到A、B两点的距离相等，则称点Q是线段AB的“似中点”．

(1)、已知A（1，0），B（3，2），在点C（1，3）、D（2，1）、E（4，﹣2）、F（3，0）中，线段AB的“似中点”是点；

(2)、直线y＝ $\sqrt{3} x + \sqrt{3}$ 与x轴交于点M，与y轴交于点N．
①若点H是线段MN的“似中点”，且在坐标轴上，求H点的坐标；

②若⊙P的半径为2，圆心P为（t，0），若⊙P上存在线段MN的“似中点”，请直接写出t的取值范围．

查看试题解析