北京市顺义区2019年中考数学二模考试试卷

试卷更新日期：2020-04-16 类型：中考模拟

进入出卷网下载

一、选择题（本题共16分，每小题2分）第1-8题均有四个选。正确选项只有一个．

1. 如图是一个几何体的展开图，这个几何体是（　　）

A、三棱锥 B、三棱柱 C、四棱锥 D、四棱柱

查看试题解析
2. 如图，数轴上的A、B、C、D四点中，与数﹣ $\sqrt{3}$ 表示的点最接近的是（）

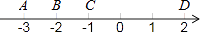A、点A B、点B C、点C D、点D

查看试题解析
3. 中国一直高度重视自主创新能力，从2000年以来，中国全社会研发经费投入以年均近20%的速度增长，到2017年，这一投入达到1.76万亿元人民币，位居全球第二．将1.76万亿用科学记数法表示应为（　　）

A、1.76×10⁸ B、1.76×10¹¹ C、1.76×10¹² D、1.76×10¹³

查看试题解析
4. 如图，把一块直角三角板的直角顶点放在直尺的一边上，若∠1＝50°，则∠2的度数为（　　）

A、50° B、40° C、30° D、25°

查看试题解析
5. 为迎接“六一”儿童节，某儿童品牌玩具专卖店购进了甲、乙两类玩具，其中甲类玩具的进价比乙类玩具的进价每个多5元，经调查：用1000元购进甲类玩具的数量与用750元购进乙类玩具的数量相同．设甲类玩具的进价为x元/个，根据题意可列方程为（　　）

A、 $\frac{1000}{x} = \frac{750}{x - 5}$ B、 $\frac{1000}{x - 5} = \frac{750}{5}$ C、 $\frac{1000}{x} = \frac{750}{x + 5}$ D、 $\frac{1000}{x + 5} = \frac{750}{x}$

查看试题解析
6. 某公司的班车在7：30，8：00，8：30从某地发车，小李在7：50至8：30之间到达车站乘坐班车，如果他到达发车站的时刻是随机的，则他等车时间不超过10分钟的概率是（　　）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
7. 规定：在平面直角坐标系xOy中，如果点P的坐标为（m，n），向量 $\vec{O P}$ 可以用点P的坐标表示为： $\vec{O P}$ ＝（m，n）．已知 $\vec{O A}$ ＝（x₁ ， y₁）， $\vec{O B}$ ＝（x₂ ， y₂），如果x₁x₂+y₁y₂＝0，那么 $\vec{O A}$ 与 $\vec{O B}$ 互相垂直．下列四组向量中，互相垂直的是（　　）

A、 $\vec{O C} = (4, - 3)$ ， $\vec{O D} = (- 3, 4)$ B、 $\vec{O E} = (- 2, 3)$ ， $\vec{O F} = (3, 2)$ C、 $\vec{O G} = (\sqrt{3}, 1)$ , $\vec{O H} = (- \sqrt{3}, 1)$ D、 $\vec{O M} = (2 \sqrt{2}, 2)$ ， $\vec{O N} = (- 2 \sqrt{2}, 2)$

查看试题解析
8. 数学课上，王老师让同学们对给定的正方形ABCD，建立合适的平面直角坐标系，并表示出各顶点的坐标．下面是4名同学表示各顶点坐标的结果：
甲同学：A（0，1），B（0，0），C（1，0），D（1，1）；

乙同学：A（0，0），B（0，﹣1），C（1，﹣1），D（1，0）；

丙同学：A（1，0），B（1，﹣2），C（3，﹣2），D（3，0）；

丁同学：A（﹣1，2），B（﹣1，0），C（0，0），D（0，2）；

上述四名同学表示的结果中，四个点的坐标都表示正确同学是（　　）

A、甲、乙、丙 B、乙、丙、丁 C、甲、丙 D、甲、乙、丙、丁

查看试题解析

二、填空题（本题共16分，每小题2分）

9. 若 $\sqrt{4 - 2 x}$ 在实数范围内有意义，则实数x的取值范围是．

查看试题解析
10. 若一个正数的平方根分别是a+1和2a﹣7，则a的值是．

查看试题解析
11. 已知a²+2a＝﹣2，则2a（2a+1）+（a+4）²的值为．

查看试题解析
12. 用一组a，b的值说明命题“若a²＞b² ，则a＞b”是不正确，这组值可以是a＝， b＝．

查看试题解析
13. 改革开放以来，由于各阶段发展重心不同，北京的需求结构经历了消费投资交替主导、投资消费双轮驱动到消费主导的变化．到2007年，北京消费率超过投资率，标志着北京经济增长由投资消费双轮驱动向消费趋于主导过渡．如图是北京1978﹣2017年投资率与消费率统计图．根据统计图回答：年，北京消费率与投资率相同；从2000年以后，北京消费率逐年上升的时间段是．

查看试题解析
14.
如图所示，在3×3的方格纸中，每个小方格都是边长为1的正方形，点O，A，B均为格点，则扇形OAB的面积大小是．

查看试题解析
15. 如图，在△ABC中，AD平分∠BAC，BD⊥AD，点E是BC的中点，连结DE，且AB＝6，AC＝10，则DE＝．

查看试题解析
16. 如图，在▱ABCD中，AB＝3，AD＝4，∠ABC＝60°，过BC的中点E作EF⊥AB，垂足为点F，与DC的延长线相交于点H，则△DEF的面积是．

查看试题解析

三、解答题（本题共68分）

17. 计算： $\sqrt{18} - 4 \cos 45 ° + {(\frac{1}{2})}^{- 2} - | 1 - \sqrt{3} |^{0}$ ．

查看试题解析
18. 解不等式组 ${\begin{cases} 2 (x + 1) < x + 5 \\ \frac{x + 7}{3} \leq x + 3 \end{cases}$ ，并写出它的非负整数解．

查看试题解析
19. 下面是小明设计的“作三角形的高线”的尺规作图过程．
已知：△ABC．

求作：BC边上的高线．

作法：如图2，

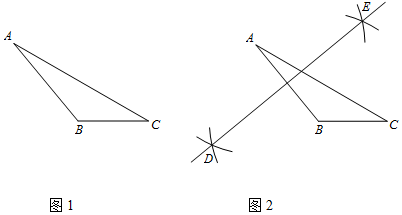
①分别以A，B为圆心，大于 $\frac{1}{2}$ AB长为半径画弧，两弧交于点D，E；

②作直线DE，与AB交于点F，以点F为圆心，FA长为半径画圆，交CB的延长线于点G；

③连接AG．

所以线段AG就是所求作的BC边上的高线．

根据小明设计的尺规作图过程，

(1)、使用直尺和圆规，补全图形；（保留作图痕迹）

(2)、完成下面证明．
证明：连接DA，DB，EA，EB，

∵DA＝DB，

∴点D在线段AB的垂直平分线上（）（填推理的依据）．

∵＝，

∴点E在线段AB的垂直平分线上．

∴DE是线段AB的垂直平分线．

∴FA＝FB．

∴AB是⊙F的直径．

∴∠AGB＝90°（）（填推理的依据）．

∴AG⊥BC

即AG就是BC边上的高线．

查看试题解析
20. 已知：关于x的方程mx²+（m﹣3）x﹣3＝0（m≠0）．

(1)、求证：方程总有两个实数根；

(2)、如果m为正整数，且方程的两个根均为整数，求m的值．

查看试题解析
21. 已知：如图，在四边形ABCD中，AD∥BC，∠A＝90°，BD＝BC，CE⊥BD于E．

(1)、求证：BE＝AD；

(2)、若∠DCE＝15°，AB＝2，求在四边形ABCD的面积．

查看试题解析
22. 已知：如图，在△ABC中，∠ACB＝90°，以BC为直径的⊙O交AB于点D，E为 $\overset{⌢}{B D}$ 的中点．

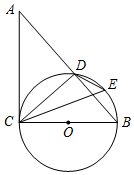(1)、求证：∠ACD＝∠DEC；

(2)、延长DE、CB交于点P，若PB＝BO，DE＝2，求PE的长．

查看试题解析
23. 如图，在平面直角坐标系xOy中，直线y＝kx+k与双曲线y＝ $\frac{4}{x}$ （x＞0）交于点A（1，a）．

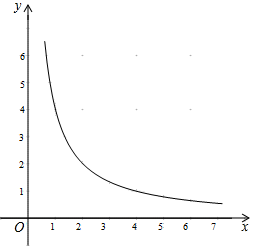(1)、求a，k的值；

(2)、已知直线l过点D（2，0）且平行于直线y＝kx+k，点P（m，n）（m＞3）是直线l上一动点，过点P分别作x轴、y轴的平行线，交双曲线y＝ $\frac{4}{x}$ （x＞0）于点M、N，双曲线在点M、N之间的部分与线段PM、PN所围成的区域（不含边界）记为W．横、纵坐标都是整数的点叫做整点．
①当m＝4时，直接写出区域W内的整点个数；

②若区域W内的整点个数不超过8个，结合图象，求m的取值范围．

查看试题解析
24. 丁老师为了解所任教的两个班的学生数学学习情况，对数学进行了一次测试，获得了两个班的成绩（百分制），并对数据（成绩）进行整理、描述和分析，下面给出了部分信息．
①A、B两班学生（两个班的人数相同）数学成绩不完整的频数分布直方图如下（数据分成5组：x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100）：

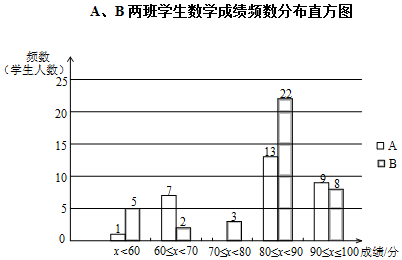
②A、B两班学生测试成绩在80≤x＜90这一组的数据如下：

A班：80 80 82 83 85 85 86 87 87 87 88 89 89

B班：80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89

③A、B两班学生测试成绩的平均数、中位数、方差如下：

平均数

中位数

方差

A班

80.6

m

96.9

B班

80.8

n

153.3

根据以上信息，回答下列问题：

(1)、补全数学成绩频数分布直方图；

(2)、写出表中m、n的值；

(3)、请你对比分析A、B两班学生的数学学习情况（至少从两个不同的角度分析）．

查看试题解析

25. 如图，在半圆弧

\overset{⌢}{A B}

中，直径AB＝6cm，点M是AB上一点，MB＝2cm，P为AB上一动点，PC⊥AB交

\overset{⌢}{A B}

于点C，连接AC和CM，设A、P两点间的距离为xcm，A、C两点间的距离为y₁cm，C、M两点间的距离为y₂cm．

小东根据学习函数的经验，分别对函数y₁、y₂随自变量x的变化而变化的规律进行了探究：

下面是小东的探究过程，请补充完整：

(1)、按照下表中自变量x的值进行取点、画图、测量，分别得到了y₁ ， y₂与x的几组对应值；

x/cm	0	1	2	3	4	5	6
y₁/cm	0	2.45	3.46		4.90	5.48	6
y₂/cm	4	3.74	3.46	3.16	2.83	2.45	2

(2)、在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x，y₁），（x，y₂），并画出函数y₁ ， y₂的图象；

(3)、结合函数图象，解决问题：

①当AC＞CM时，线段AP的取值范围是；

②当△AMC是等腰三角形时，线段AP的长约为．

查看试题解析

26. 在平面直角坐标系xOy中，抛物线y＝mx²+2mx﹣3（m＞0）与x轴交于A、B两点（点A在点B左侧），与y轴交于点C，该抛物线的顶点D的纵坐标是﹣4．

(1)、求点A、B的坐标；

(2)、设直线与直线AC关于该抛物线的对称轴对称，求直线的表达式；

(3)、平行于x轴的直线b与抛物线交于点M（x₁ ， y₁）、N（x₂ ， y₂），与直线交于点P（x₃ ， y₃）．若x₁＜x₃＜x₂ ，结合函数图象，求x₁+x₂+x₃的取值范围．

查看试题解析
27. 已知：在△ABC中，∠BAC＝90°，AB＝AC.

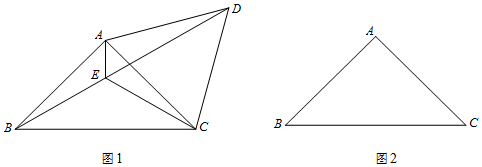(1)、如图1，将线段AC绕点A逆时针旋转60°得到AD，连结CD、BD，∠BAC的平分线交BD于点E，
连结CE.

①求证：∠AED＝∠CED；

②用等式表示线段AE、CE、BD之间的数量关系（直接写出结果）；

(2)、在图2中，若将线段AC绕点A顺时针旋转60°得到AD，连结CD、BD，∠BAC的平分线交BD的延长线于点E，连结CE.请补全图形，并用等式表示线段AE、CE、BD之间的数量关系，并证明.

查看试题解析
28. 对于平面直角坐标系xOy中的任意两点M（x₁ ， y₁），N（x₂ ， y₂），给出如下定义：点M与点N的“折线距离”为：d（M，N）＝|x₁﹣x₂|+|y₁﹣y₂|．

例如：若点M（﹣1，1），点N （2，﹣2），则点M与点N的“折线距离”为：d（M，N）＝|﹣1﹣2|+|1﹣（﹣2）|＝3+3＝6．

根据以上定义，解决下列问题：

(1)、已知点P （3，﹣2）．
①若点A（﹣2，﹣1），则d（P，A）＝；

②若点B（b，2），且d（P，B）＝5，则b＝；

(2)、已知点C（m，n）是直线y＝﹣x上的一个动点，且d（P，C）＜3，求m的取值范围．

(3)、⊙F的半径为1，圆心F的坐标为（0，t），若⊙F上存在点E，使d（E，O）＝2，直接写出t的取值范围．

查看试题解析

	平均数	中位数	方差
A班	80.6	m	96.9
B班	80.8	n	153.3