北京市石景山区2019年中考数学一模考试试卷
试卷更新日期：2020-04-16 类型：中考模拟
一、选择题（本题共16分，每小题2分）第1-8题均有四个选。正确选项只有一个．
-
1. 在北京筹办2022年冬奥会期间，原首钢西十筒仓一片130000平方米的区域被改建为北京冬奥组委办公区．将130000用科学记数法表示应为（ ）A、13×104 B、1.3×105 C、0.13×106 D、1.3×1072.
如图是某几何体的三视图，该几何体是（ ）
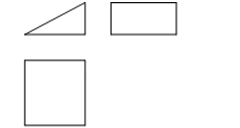A、三棱柱 B、三棱锥 C、长方体 D、正方体3. 实数a，b，c在数轴上对应点的位置如图所示，则正确结论是（ ）
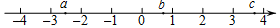A、a＞﹣2 B、|b|＞1 C、a+c＞0 D、abc＞04. 下列图案中，是中心对称图形的为（ ）A、
B、
C、
D、
5. 如图，直线AB∥CD，直线EF分别与AB，CD交于点E，F，EG平分∠BEF，交CD于点G，若∠1＝70°，则∠2的度数是（ ）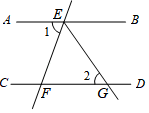
A、60° B、55° C、50° D、45°6. 为了保障艺术节表演的整体效果，某校在操场中标记了几个关键位置，如图是利用平面直角坐标系画出的关键位置分布图，若这个坐标系分别以正东、正北方向为x轴、y轴的正方向，表示点A的坐标为（1，﹣1），表示点B的坐标为（3，2），则表示其他位置的点的坐标正确是（ ）
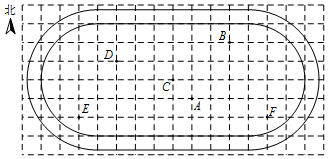A、C（﹣1，0） B、D（﹣3，1） C、E（﹣2，﹣5） D、F（5，2）7. 下面的统计图反映了我国五年来农村贫困人口的相关情况，其中“贫困发生率”是指贫困人口占目标调查人口的百分比．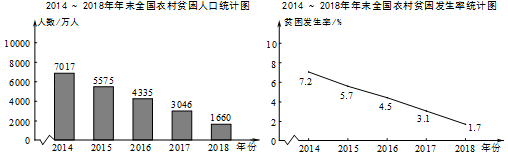
（以上数据来自国家统计局）
根据统计图提供的信息，下列推断不合理的是（ ）
A、与2017年相比，2018年年末全国农村贫困人口减少了1386万人 B、2015～2018年年末，与上一年相比，全国农村贫困发生率逐年下降 C、2015～2018年年末，与上一年相比，全国农村贫困人口的减少量均超过1000万 D、2015～2018年年末，与上一年相比，全国农村贫困发生率均下降1.4个百分点8. 如图，在平面直角坐标系xOy中，△AOB可以看作是由△OCD经过两次图形的变化（平移、轴对称、旋转）得到的，这个变化过程不可能是（ ）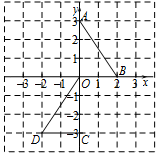
A、先平移，再轴对称 B、先轴对称，再旋转 C、先旋转，再平移 D、先轴对称，再平移二、填空题（本题共16分，每小题2分）
-
9. 请你写出一个大于2小于3的无理数是 ．10. 如图所示的网格是正方形网格，点P到射线OA的距离为m，点P到射线OB的距离为n，则mn．（填“＞”，“＝”或“＜”）
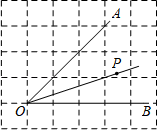11. 一个不透明盒子中装有3个红球、5个黄球和2个白球，这些球除了颜色外无其他差别．从中随机摸出一个球，恰好是红球的概率为 ．12. 正多边形的一个内角为135°，则该正多边形的边数为13. 如图，在△ABC中，D，E分别是AB，AC上的点，DE∥BC．若AE＝6，EC＝3，DE＝8，则BC＝ ．
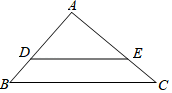14. 如果m2﹣m﹣3＝0，那么代数式 的值是 ．15. 我国古代数学著作《算法统宗》中记载了“绳索量竿”问题，其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺．求绳索和竿的长度．设绳索长x尺，竿长y尺，可列方程组为 ．16. 如图，AB是⊙O的一条弦，P是⊙O上一动点（不与点A，B重合），C，D分别是AB，BP的中点．若AB＝4，∠APB＝45°，则CD长的最大值为 ．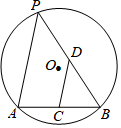
三、解答题（本题共68分，第17-22题，每小题5分，第23-26题，每小题5分，第27，28题，每小题5分）解答应写出文字说明、演算步骤或证明过程．
-
17. 下面是小立设计的“过直线外一点作这条直线的平行线”的尺规作图过程．
已知：如图1，直线l及直线l外一点A．
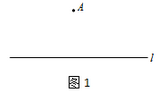
求作：直线AD，使得AD∥l．
作法：如图2，
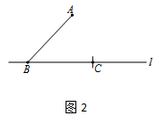
①在直线l上任取一点B，连接AB；
②以点B为圆心，AB长为半径画弧，交直线l于点C；
③分别以点A，C为圆心，AB长为半径画弧，两弧交于点D（不与点B重合）；
④作直线AD．
所以直线AD就是所求作的直线．
根据小立设计的尺规作图过程，
(1)、 使用直尺和圆规，补全图形；（保留作图痕迹）(2)、完成下面的证明．（说明：括号里填推理的依据）证明：连接CD．
∵AD＝CD＝BC＝AB，
∴四边形ABCD是（）．
∴AD∥l（）．
18. 计算： ．19. 解不等式组：20. 关于x的一元二次方程x2﹣（m+3）x+m+2＝0．(1)、求证：方程总有两个实数根；(2)、若方程的两个实数根都是正整数，求m的最小值．21. 如图，在△ABC中，∠ACB＝90°，D为AB边上一点，连接CD，E为CD中点，连接BE并延长至点F，使得EF＝EB，连接DF交AC于点G，连接CF．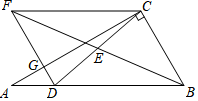
(1)、求证：四边形DBCF是平行四边形；(2)、若∠A＝30°，BC＝4，CF＝6，求CD的长．22. 如图，AB是⊙O的直径，过⊙O上一点C作⊙O的切线CD，过点B作BE⊥CD于点E，延长EB交⊙O于点F，连接AC，AF．(1)、求证：CE＝ AF；(2)、连接BC，若⊙O的半径为5，tan∠CAF＝2，求BC的长．
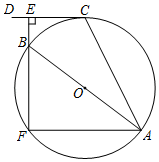23. 如图，在平面直角坐标系xOy中，函数 的图象经过点A（﹣1，6），直线y＝mx﹣2与x轴交于点B（﹣1，0）．
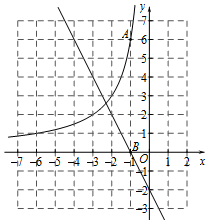(1)、求k，m的值；(2)、过第二象限的点P（n，﹣2n）作平行于x轴的直线，交直线y＝mx﹣2于点C，交函数 的图象于点D．①当n＝﹣1时，判断线段PD与PC的数量关系，并说明理由；
②若PD≥2PC，结合函数的图象，直接写出n的取值范围．
24. 如图，Q是 上一定点，P是弦AB上一动点，C为AP中点，连接CQ，过点P作PD∥CQ交 于点D，连接AD，CD．已知AB＝8cm，设A，P两点间的距离为xcm，C，D两点间的距离为ycm．（当点P与点A重合时，令y的值为1.30）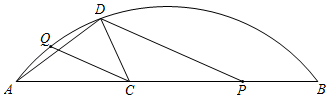
小荣根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．
下面是小荣的探究过程，请补充完整：
(1)、按照下表中自变量x的值进行取点、画图、测量，得到了y与x的几组对应值：x/cm
0
1
2
3
4
5
6
7
8
y/cm
1.30
1.79
1.74
1.66
1.63
1.69
2.08
2.39
(2)、建立平面直角坐标系，描出以补全后的表中各组对应值为坐标的点，画出该函数的图象；
(3)、结合函数图象，解决问题：当DA⊥DP时，AP的长度约为cm．25. 为了调查学生对垃圾分类及投放知识的了解情况，从甲、乙两校各随机抽取40名学生进行了相关知识测试，获得了他们的成绩（百分制），并对数据（成绩）进行了整理、描述和分析．下面给出了部分信息．a．甲、乙两校40名学生成绩的频数分布统计表如下：
成绩x
学校
50≤x＜60
60≤x＜70
70≤x＜80
80≤x＜90
90≤x≤100
甲
4
11
13
10
2
乙
6
3
15
14
2
（说明：成绩80分及以上为优秀，70～79分为良好，60～69分为合格，60分以下为不合格）
b．甲校成绩在70≤x＜80这一组的是：70 70 70 71 72 73 73 73 74 75 76 77 78
c．甲、乙两校成绩的平均分、中位数、众数如下：
学校
平均分
中位数
众数
甲
74.2
n
85
乙
73.5
76
84
根据以上信息，回答下列问题：
(1)、写出表中n的值；(2)、在此次测试中，某学生的成绩是74分，在他所属学校排在前20名，由表中数据可知该学生是校的学生（填“甲”或“乙”），理由是；(3)、假设乙校800名学生都参加此次测试，估计成绩优秀的学生人数．26. 在平面直角坐标系xOy中，直线y＝kx+1（k≠0）经过点A（2，3），与y轴交于点B，与抛物线y＝ax2+bx+a的对称轴交于点C（m，2）．(1)、求m的值；(2)、求抛物线的顶点坐标；(3)、N（x1 ， y1）是线段AB上一动点，过点N作垂直于y轴的直线与抛物线交于点P（x2 ， y2），Q（x3 ， y3）（点P在点Q的左侧）．若x2＜x1＜x3恒成立，结合函数的图象，求a的取值范围．27. 如图，在等边△ABC中，D为边AC的延长线上一点（CD＜AC），平移线段BC，使点C移动到点D，得到线段ED，M为ED的中点，过点M作ED的垂线，交BC于点F，交AC于点G．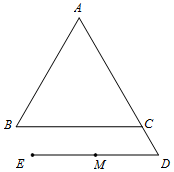
(1)、依题意补全图形；(2)、求证：AG＝CD；(3)、连接DF并延长交AB于点H，用等式表示线段AH与CG的数量关系，并证明．28. 在平面直角坐标系xOy中，正方形ABCD的顶点分别为A（0，1），B（﹣1，0），C（0，﹣1），D（1，0）．对于图形M，给出如下定义：P为图形M上任意一点，Q为正方形ABCD边上任意一点，如果P，Q两点间的距离有最大值，那么称这个最大值为图形M的“正方距”，记作d（M）．(1)、已知点E（0，4），①直接写出d（点E）的值；
②直线y＝kx+4（k≠0）与x轴交于点F，当d（线段EF）取最小值时，求k的取值范围；
(2)、⊙T的圆心为T（t，3），半径为1．若d（⊙T）＜6，直接写出t的取值范围．