湖北省武汉市青山区2020年九年级下学期数学3月月考试卷

试卷更新日期：2020-04-16 类型：月考试卷

进入 出卷网 下载

一、选择题（共10小题，每小题3分，共30分）

  • 1. 下列四个实数中，最小的是（ ）
    A、－2 B、－5 C、1 D、4

    查看试题解析

  • 2. 式子 x+3 在实数范围内有意义，则 x 的取值范围是（           ）
    A、x＞﹣3 B、x≥3 C、               x≥﹣3 D、x≤﹣3

    查看试题解析

  • 3. 下列说法正确的是（  ）
    A、为了解一批灯泡的使用寿命，宜采用全面调查方式 B、掷两枚质地均匀的硬币，两枚硬币都是正面朝上的概率为0.5 C、掷一枚质地均匀的正方体骰子，5点朝上是必然事件 D、甲、乙两人在相同条件下各射击10次，他们成绩的平均数相同，方差分别 S甲2 ＝0.4， S乙2 ＝0.6，则甲的射击成绩较稳定

    查看试题解析

  • 4. 下列四个图案中，是中心对称图形的是（    ）
    A、 B、 C、 D、

    查看试题解析

  • 5. 如图，在下列四个几何体中，它的三视图不完全相同的是（）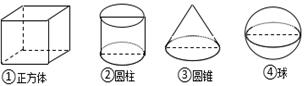

    A、①② B、②③ C、①③ D、③④

    查看试题解析

  • 6. 《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等．交易其一，金轻十三两．问金、银一枚各重几何？”意思是：甲袋中装有黄金 9 枚，乙袋中装有白银 11 枚，称重两袋相等．两袋互相交换 1 枚后，甲袋比乙袋轻了 13 两．问黄金、白银每枚各重多少两？设每枚黄金重 x 两，每枚白银重 y 两，列方程组（    ）
    A、{9x=11y(10y+x)−(8x+y)=13 B、{10y+x=8x+y9x+13=11y C、{11x=9y(10y+x)−(8x+y)=13 D、{9x=13y(8x+y)−(10y+x)=13

    查看试题解析

  • 7. 从－1，2，3，－6 这四个数中随机取两个数，分别记作 m，n，点（m，n）在函数 y= 6x

    图象上的概率是（ ）．

    A、34 B、23 C、12 D、13

    查看试题解析

  • 8. 正方形ABCD的边AB上有一动点E，以EC为边作矩形ECFG，且边FG过点D，在点E从点A移动到点B的过程中，矩形ECFG的面积（   ）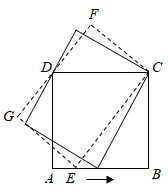

    A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变

    查看试题解析

  • 9. 反比例函数 y=k−1x 与一次函数y＝k（x+1）（其中 x 为自变量，k 为常数）在同一坐标中的图像可能是（     ）
    A、 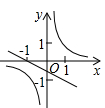B、 C、 D、

    查看试题解析

  • 10. 已知有理数a≠1，我们把 11−a 称为a的差倒数，如：2 的差倒数是 11−2 差倒数是-1，-1的差倒数是 11−(−1)=12 如果a1＝－2，a2是a1的差倒数，a3是a2的差倒数，a4是a3的差倒数，„，依此类推，那么a1＋a2＋„＋a100的值是（ ）
    A、－7.5 B、7.5 C、5.5 D、－5.5

    查看试题解析

二、多项选择题（6小题，每小题3分，共18分）说明：下列各题的结果有一个或者多 个，请把所有可能的结果选出来，漏选、错选、不选都得0分．

  • 11. 计算 32 － 18 的结果是（     ）
    A、2 B、2 2 C、3 D、2 3

    查看试题解析

  • 12. 计算： 2xx−2−4x−2 =（     ）
    A、1 B、2 C、x+2x−2 D、2x−2

    查看试题解析

  • 13. 定义：等腰三角形的顶角与其一个底角的度数的比值 k 称为这个等腰三角形的特征值

    等腰ABC 中，∠A＝80°，则等腰△ABC 的特征值 k＝（        ）

    A、58 B、85 C、14 D、4

    查看试题解析

  • 14. 如图，矩形DEFG的边EF在△ABC的边BC上，顶点D，G分别在边AB，AC上，AH⊥BC，垂足为H，AH交DG于点P．已知BC＝6，AH＝4．当矩形DEFG面积最大时，HP的长是（     ）

    A、1 B、2 C、3 D、4

    查看试题解析

  • 15. 抛物线 y＝x2＋bx+3 的对称轴为直线 x＝1．若关于 x 的一元二次方程 x2＋bx+3－t＝0（t为实数）在－1＜x＜4 的范围内有且只有一个实数根（两个相等的实数根视为一个实数根），则 t 的取值范围是 B，（     ）
    A、2≤t＜11 B、t＝2 C、6≤t＜11 D、6＜t≤11

    查看试题解析

  • 16. 如图，A，B，C，D 为一直线上 4 个点，BC＝3，△BCE 为等边三角形，⊙O 过 A，D， E 三点，且∠AOD＝120°．设 AB＝x，CD＝y，则y与 x的函数关系式（     ）．

    A、y=3x B、y=19x C、y=3x+3 D、y=9x

    查看试题解析

三、解答题（共8题，共72分）

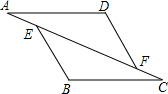
  • 17. 计算：x•x3+（2x2）2﹣2x5÷x．

    查看试题解析

  • 18. 如图，已知：点 A，E，F，C 在同一直线上，AE＝CF，∠B＝∠D，AD∥BC． 求证：AD＝BC．

    查看试题解析

  • 19. 某同学进行社会调查，随机抽查了某个小区的 200 户家庭的年收入，并绘制成统计图（如图）．请你根据统计图给出的信息回答：

    (1)、样本数据的中位数是 ， 众数是 ；
    (2)、这 200 户家庭的平均年收入为万 元 ；
    (3)、在平均数、中位数两数中，更能反映这个小区家庭的年收入水平．
    (4)、如果该小区有 1200 户住户，请你根据抽样调查的结果估计该小区有户家庭 的 年 收 入 低 于1.3万元？

    查看试题解析

  • 20. 如图，在下列18×7的网格中，横、纵坐标均为整数的点叫做格点，例如A（－8，0）、B（－4，3）都是格点.

    (1)、直接写出△ABO的形状；
    (2)、要求在下图中仅用无刻度的直尺画图：将△ABO绕点O顺时针旋转得△DEO，且点B的对应点E落在x轴正半轴上．

    操作如下：

    第一步：在x正半轴上找一个格点E，使OE＝OB；
    第二步：找一个格点F，使∠EOF＝∠AOB；
    第三步：找一个格点M，作直线AM交直线OF于D，连DE，则△DEO即为所作出的图形.

    请你按以上操作完成画图．并直接写出点E，F，M三点的坐标．

    查看试题解析

  • 21. 如图，△ABC内接于⊙O，BC是⊙O的直径，弦AF交BC于点E，∠CAF＝2∠B．


    (1)、求证：AE＝AC；
    (2)、若⊙O的半径为4，E是OB的中点，求EF的长．

    查看试题解析

  • 22. 公司以10元/千克的价格收购一批产品进行销售，经过市场调查获悉，日销售量y（千克）是销售价格x（元/千克）的一次函数，部分数据如表

    (1)、直接写出y与x之间的函数表达式；
    (2)、求日销售利润为1500元时的销售价格；
    (3)、若公司每销售1千克产品需另行支出a元（0＜a＜10）的费用，当20≤x≤25时，公司的日获利润的最大值为1215元，求a的值．

    查看试题解析

  • 23. 如图1，AB⊥BC，分别过点A，C作BM的垂线，垂足分别为M，N．

    (1)、求证：BM·BC＝AB·CN；
    (2)、若AB＝BC．

    ①如图2，若BM＝MN，过点A作AD∥BC交CN的延长线于点D，求DN∶CN的值；

    ②如图3，若BM＞MN，延长BN至点E，使BM＝ME，过点A作AF∥BC交CE的延长线于点F，若E是CF的中点，且CN＝1，直接写出线段AF的长.

    查看试题解析

  • 24. 抛物线y＝﹣x2＋bx＋c与x轴交于A，B两点（点A在B左边），与y轴交于点C.


    (1)、如图1，已知A（－1，0），B（3，0）．

    ①直接写出抛物线的解析式；

    ②点H在x轴上，D（1，0），连接AC，DC，HC，若CD平分∠ACH，求点H的坐标；

    (2)、如图2，直线y＝﹣1与抛物线y＝﹣x2＋bx＋c交于点D，点E，D关于x轴对称．

    ①若点D在抛物线对称轴的右侧，求证：DB⊥AE；

    ②若点D在抛物线对称轴的左侧，请直接判断，BD是否垂直AE？

    查看试题解析