河北省2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期:2017-09-08 类型:期末考试
一、选择题
-
1. 下列计算结果正确的是( )A、 + = B、3 ﹣ =3 C、 × = D、 =52. 由下列条件不能判定△ABC为直角三角形的是( )A、(b+c)(b﹣c)=a2 B、a=3+k,b=4+k,c=5+k(k>0) C、∠A+∠B=∠C D、∠A:∠B:∠C=1:3:23. 在▱ABCD中,如果∠A+∠C=160°,那么∠B等于( )A、20° B、100° C、60° D、80°4. 如图,在△ABC中,D、E分别是AB、AC的中点,BC=12,则DE的长是( )
 A、4 B、5 C、6 D、75. 如图,在▱ABCD中,AD=8,AB=6,DE平分∠ADC交BC于点E,则BE的长是( )
A、4 B、5 C、6 D、75. 如图,在▱ABCD中,AD=8,AB=6,DE平分∠ADC交BC于点E,则BE的长是( ) A、2 B、3 C、4 D、56. 已知一次函数y=kx﹣1,若y随x的增大而增大,则该函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x<ax+4的解集为( )
A、2 B、3 C、4 D、56. 已知一次函数y=kx﹣1,若y随x的增大而增大,则该函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x<ax+4的解集为( ) A、x< B、x<3 C、x> D、x>38. 已知,A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A.两人同时出发,各自到达终点后停止.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下图中正确反映s与t之间函数关系的是( )A、
A、x< B、x<3 C、x> D、x>38. 已知,A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A.两人同时出发,各自到达终点后停止.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下图中正确反映s与t之间函数关系的是( )A、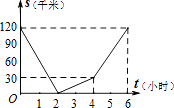 B、
B、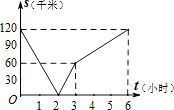 C、
C、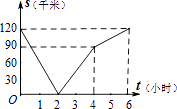 D、
D、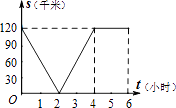
二、填空题
-
9. 要使分式 有意义,x的取值范围为 .10. 在某次数学测验中,随机抽取了10份试卷,其成绩如下:72,77,79,81,81,81,83,83,85,89,则这组数据的众数、中位数分别为 .11. 在Rt△ABC中,∠C=90°,D为BC上的一点,AD=BD=2,AB= ,则AC的长为 .12. 已知直角三角形的周长为14,斜边上的中线长为3.则直角三角形的面积是 .13. 如图,在平行四边形ABCD中,AB=10,BC=6,E、F分别是AD、DC的中点,若EF=7,则四边形EACF的周长是 .
 14. 已知一个平行四边形的一条对角线将其分为全等的两个等腰直角三角形,且这条对角线的长为8,则另一条对角线长为 .15. 已知一次函数y=kx+b的图象与直线y=﹣x+1平行,且过点(1,﹣2),那么此一次函数的解析式为 .
14. 已知一个平行四边形的一条对角线将其分为全等的两个等腰直角三角形,且这条对角线的长为8,则另一条对角线长为 .15. 已知一次函数y=kx+b的图象与直线y=﹣x+1平行,且过点(1,﹣2),那么此一次函数的解析式为 .三、解答题
-
16. 计算:( ﹣1)( +1)﹣(﹣ )﹣2+|1﹣ |﹣(π﹣2)0﹣ .17. 一次函数图象经过(3,5)和(﹣4,﹣9)两点,求这个一次函数的解析式.18. 如图,△ABC中,CD⊥AB于D,若AD=2BD,AC=6,BC=4,求BD的长.
 19. 如图,在▱ABDC中,分别取AC、BD的中点E和F,连接BE、CF,过点A作AP∥BC,交DC的延长线于点P.
19. 如图,在▱ABDC中,分别取AC、BD的中点E和F,连接BE、CF,过点A作AP∥BC,交DC的延长线于点P. (1)、求证:△ABE≌△DCF;(2)、当∠P满足什么条件时,四边形BECF是菱形?证明你的结论.20. 如图,已知,直线y=2x+3与直线y=﹣2x﹣1,求△ABC的面积.
(1)、求证:△ABE≌△DCF;(2)、当∠P满足什么条件时,四边形BECF是菱形?证明你的结论.20. 如图,已知,直线y=2x+3与直线y=﹣2x﹣1,求△ABC的面积. 21. 某商场欲购进果汁饮料和碳酸饮料共50箱,两种饮料每箱的进价和售价如下表所示.设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为W元(注:总利润=总售价﹣总进价).(1)、设商场购进碳酸饮料y箱,直接写出y与x的函数关系式;(2)、求总利润w关于x的函数关系式;(3)、如果购进两种饮料的总费用不超过2100元,那么该商场如何进货才能获利最多?并求出最大利润.
21. 某商场欲购进果汁饮料和碳酸饮料共50箱,两种饮料每箱的进价和售价如下表所示.设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为W元(注:总利润=总售价﹣总进价).(1)、设商场购进碳酸饮料y箱,直接写出y与x的函数关系式;(2)、求总利润w关于x的函数关系式;(3)、如果购进两种饮料的总费用不超过2100元,那么该商场如何进货才能获利最多?并求出最大利润.饮料
果汁饮料
碳酸饮料
进价(元/箱)
51
36
售价(元/箱)
61
43
22. 八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9
(1)、甲队成绩的中位数是分,乙队成绩的众数是分;(2)、计算乙队的平均成绩和方差;(3)、已知甲队成绩的方差是1.4,则成绩较为整齐的是队.23. 如图,在平面直角坐标系中,已知O为原点,四边形ABCD为平行四边形,A、B、C的坐标分别是A(﹣5,1),B(﹣2,4),C(5,4),点D在第一象限. (1)、写出D点的坐标;(2)、求经过B、D两点的直线的解析式,并求线段BD的长;(3)、将平行四边形ABCD先向右平移1个单位长度,再向下平移1个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少?并求出平行四边形ABCD与四边形A1B1C1D1重叠部分的面积.
(1)、写出D点的坐标;(2)、求经过B、D两点的直线的解析式,并求线段BD的长;(3)、将平行四边形ABCD先向右平移1个单位长度,再向下平移1个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少?并求出平行四边形ABCD与四边形A1B1C1D1重叠部分的面积.