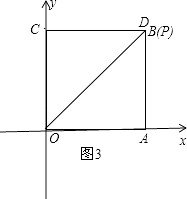贵州省黔东南州2016-2017学年八年级下学期数学期末考试试卷

试卷更新日期：2017-09-08 类型：期末考试

进入出卷网下载

一、选择题

1. 计算 $\sqrt{9}$ 的结果为（）

A、3 B、﹣3 C、±3 D、4.5

查看试题解析
2. 下列运算正确的是（）

A、 $\sqrt{{(- 2)}^{2}} = - 2$ B、 $\sqrt{x^{2}} = x$ C、 $\sqrt{2} + \sqrt{5} = \sqrt{7}$ D、 $\sqrt{8} = 2 \sqrt{2}$

查看试题解析
3. 下列各组数据中的三个数作为三角形的边长，其中能构成直角三角形的是（）

A、1，2，3 B、 $\sqrt{2}$ ， $\sqrt{3}$ ， $\sqrt{5}$ C、3，5，7 D、5，7，9

查看试题解析
4. 某品牌鞋店在一个月内销售某款女鞋，各种尺码鞋的销量如下表所示：
尺码/厘米
22.5
23
23.5
24
24.5
销售量/双
35
40
30
17
8
通过分析上述数据，对鞋店业主的进货最有意义的是（）

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
5. 如图，在Rt△ABC中，∠ACB=90°．若AB=10，则正方形ADEC和正方形BCFG的面积和为（）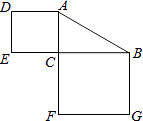

A、100 B、120 C、140 D、160

查看试题解析
6. 平行四边形的两条对角线分别为6和10，则其中一条边x的取值范围为（）

A、4＜x＜6 B、2＜x＜8 C、0＜x＜10 D、0＜x＜6

查看试题解析
7. 下列条件中，不能判断四边形ABCD是平行四边形的是（　　）

A、∠A=∠C，∠B=∠D B、AB∥CD，AB=CD C、AB=CD，AD∥BC D、AB∥CD，AD∥BC

查看试题解析
8. 如图，直线y₁=k₁x+b₁与直线y₂=k₂x+b₂相交于点P，则关于x的不等式k₁x+b₁＞k₂x+b₂的解集为（）

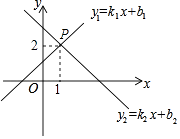A、x＞1 B、x＜1 C、x＞2 D、x＜2

查看试题解析
9. 已知一次函数y=kx+b﹣x的图象与x轴的正半轴相交，且函数值y随自变量x的增大而增大，则k、b的取值情况为（）

A、k＞0，b＞0 B、k＞0，b＜0 C、k＞l，b＜0 D、k＞l，b＞0

查看试题解析
10. 如图，将边长为8cm正方形纸片ABCD折叠，使点D落在BC边的中点E处，点A落在点F处，折痕为MN，则线段CN的长是（）

A、6cm B、5cm C、4cm D、3cm

查看试题解析

二、填空题

11. 函数y= $\sqrt{x - 1}$ 的自变量x的取值范围是．

查看试题解析
12. 直线y=kx+b过点（2，0）和点（0，﹣3），则关于x的方程kx+b=0的解是．

查看试题解析
13. 在数轴上表示实数a的点如图所示，化简 $\sqrt{{(a - 5)}^{2}}$ +|a﹣2|的结果为．

查看试题解析
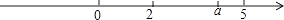14. 如图，O是矩形ABCD的对角线AC的中点，M是AD的中点．若AB=5，AD=12，则四边形ABOM的周长为．

查看试题解析
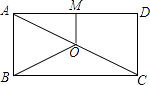15. 若一次函数y=（2m﹣1）x+3﹣2m的图象经过一、二、四象限，则m的取值范围是．

查看试题解析
16. 如图，在△ABC中，AB=3，AC=4，BC=5，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为．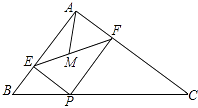

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{8}$ ﹣6 $\sqrt{\frac{1}{2}}$ + $\sqrt{12}$ ﹣| $\sqrt{2}$ ﹣ $\sqrt{3}$ |；

(2)、（2 $\sqrt{3}$ ﹣1）（2 $\sqrt{3}$ +1）﹣（1﹣2 $\sqrt{3}$ ）² ．

查看试题解析
18. 某校为了了解九年级上学期期末考试数学成绩，从九年级学生中随机抽取了部分学生进行调查，并将所抽取的学生数学成绩（成绩均为整数）分为A、B、C、D、E五个等级，A：50.5～60.5，B：60.5～70.5，C：70.5～80.5，D：80.5～90.5，E：90.5～100.5，并绘制了如图所示的频数分布直方图和扇形统计图，请你根据统计图提供的信息解答下列问题：

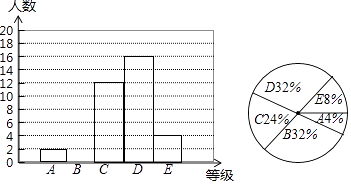(1)、这次抽样调查共抽取了多少名学生？

(2)、请把频数分布直方图补充完整；

(3)、这次期末考试数学成绩的中位数落在哪个等级内？

(4)、该校九年级有800名学生，若规定80分以上（不含80分）为良好，试估计九年级有多少名学生的数学成绩为良好？

查看试题解析
19. 如图，▱ABCD中，点E，F在对角线BD上，且BE=DF，求证：

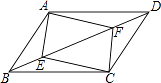(1)、AE=CF；

(2)、四边形AECF是平行四边形．

查看试题解析
20. 如图，在正方形ABCD中，E是BC的中点，F是CD上一点，且CF= $\frac{1}{4}$ CD，求证：∠AEF=90°．

查看试题解析
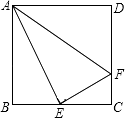21. 如图，直线l₁：y=kx+b与y轴交于点A（0，7），直线l₂：y=3x﹣3交y轴于点B，交直线l₁于点P（2，m）．

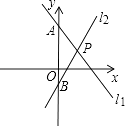(1)、求直线l₁的解析式；

(2)、求△PAB的面积．

查看试题解析
22. 如图，在△ABC中，∠ACB=90°，M、N分别是AB、AC的中点，延长BC至点D，使CD= $\frac{1}{3}$ BD．连接DM、DN、MN．若AB=6，求DN的长．

查看试题解析
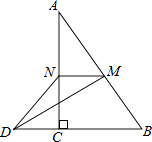23. 现代互联网技术的广泛应用，催生了快递行业的高速发展．小明计划给朋友快递一部分物品，经了解有甲、乙两家快递公司比较合适．甲公司表示：快递物品不超过1千克的，按每千克22元收费；超过1千克，超过的部分按每千克15元收费．乙公司表示：按每千克16元收费，另加包装费3元．设小明快递物品x千克．

(1)、请分别写出甲、乙两家快递公司快递该物品的费用y（元）与x（千克）之间的函数关系式；

(2)、小明选择哪家快递公司更省钱？

查看试题解析
24. 如图，将边长为4的正方形OABC置于平面直角坐标系中，点P在边OA上从O向A运动，连接CP交对角线OB于点Q，连接AQ．

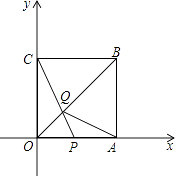(1)、求证：△OCQ≌△OAQ；

(2)、当点Q的坐标为（ $\frac{4}{3}$ ， $\frac{4}{3}$ ）时，求点P的坐标；

(3)、若点P在边OA上从点O运动到点A后，再继续在边AB上从A运动到点B，在整个过运动过程中，若△OCQ恰为等腰三角形，请直接写出所有满足条件的点P的坐标．

查看试题解析

尺码/厘米	22.5	23	23.5	24	24.5
销售量/双	35	40	30	17	8