甘肃省张掖市临泽二中2016-2017学年八年级下学期数学期末考试试卷

试卷更新日期：2017-09-08 类型：期末考试

进入出卷网下载

一、选择题

1. 下列各式 $\frac{1}{5}$ （1﹣x）， $\frac{4 x}{π - 3}$ ， $\frac{x^{2} - y^{2}}{2}$ ， $\frac{1}{x}$ +x， $\frac{5 x^{2}}{x}$ ，其中分式共有（）个．

A、2 B、3 C、4 D、5

查看试题解析
2. 下面平行四边形不具有的性质是（）

A、对角线互相平分 B、两组对边分别相等 C、对角线相等 D、相邻两角互补

查看试题解析
3. 已知等腰三角形的两边长分别为5cm、2cm，则该等腰三角形的周长是（　　）

A、7cm B、9cm C、12cm或者9cm D、12cm

查看试题解析
4. 已知两个不等式的解集在数轴上如图表示，那么这个解集为（）

A、x≥﹣1 B、x＞1 C、﹣3＜x≤﹣1 D、x＞﹣3

查看试题解析
5. 下列各式从左到右的变形中，是因式分解的为（）

A、x（a﹣b）=ax﹣bx B、x²﹣1+y²=（x﹣1）（x+1）+y² C、x²﹣1=（x+1）（x﹣1） D、ax+bx+c=x（a+b）+c

查看试题解析
6. 如图，▱ABCD的周长是22cm，△ABC的周长是17cm，则AC的长为（）

A、5 cm B、6 cm C、7 cm D、8 cm

查看试题解析
7. 下列多项式中，可以用平方差公式分解因式的是（）

A、a²+4 B、a²﹣ab² C、﹣a²+4 D、﹣a²﹣4

查看试题解析
8. 如图，在四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定四边形ABCD为平行四边形的是（）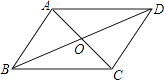

A、AB∥CD，AD∥BC B、OA=OC，OB=OD C、AD=BC，AB∥CD D、AB=CD，AD=BC

查看试题解析
9. 关于x的方程 $\frac{m - 1}{x - 1}$ ﹣ $\frac{x}{x - 1}$ =0有增根，则m的值是（）

A、2 B、﹣2 C、1 D、﹣1

查看试题解析
10. 已知△ABC的周长为1，连接△ABC的三边中点构成第二个三角形，再连接第二个三角形的三边中点构成第三个三角形，依此类推，第2010个三角形的周长是（）

A、 $\frac{1}{2008}$ B、 $\frac{1}{2009}$ C、 $\frac{1}{2^{2008}}$ D、 $\frac{1}{2^{2009}}$

查看试题解析

二、填空题

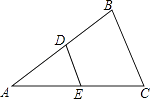
11. 分解因式：x³y﹣2x²y²+xy³= ．

查看试题解析
12. 不等式7﹣x＞1的正整数解为：．

查看试题解析
13. 化简 $\frac{2 x + 2 y}{5 a^{2} b} \cdot \frac{10 a b^{2}}{x^{2} - y^{2}}$ 的结果为．

查看试题解析
14. 如果9x²+kx+25是一个完全平方式，那么k的值是．

查看试题解析
15. 如图，△ABC中，AD=BD，AE=EC，BC=6，则DE= ．

查看试题解析
16. 一个多边形的每一个内角都是108°，你们这个多边形的边数是．

查看试题解析
17. 如图，等腰△ABC中，AB=AC，∠DBC=15°，AB的垂直平分线MN交AC于点D，则∠A的度数是．

查看试题解析
18. 若分式 $\frac{| x | - 3}{x - 3}$ 的值为零，则x= ．

查看试题解析
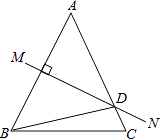19. 如图所示，在△ABC中，∠B=90°，AB=3，AC=5，将△ABC折叠，使点C与点A重合，折痕为DE，则△ABE的周长为．

查看试题解析
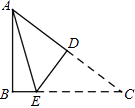20. 如图，在▱ABCD中，AE⊥BC于E，AF⊥CD于F，若AE=4，AF=6，▱ABCD的周长为40，则▱ABCD的面积为．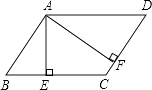

查看试题解析

三、作图题：

21. 如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点，△ABC的顶点均在格点上，请按要求完成下列步骤：

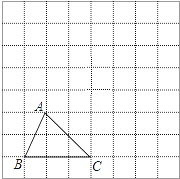
⑴画出将△ABC向上平移3个单位后得到的△A₁B₁C₁；

⑵画出将△A₁B₁C₁绕点C₁按顺时针方向旋转90°后所得到的△A₂B₂C₁ ．

查看试题解析

四、解答题：

22. 解方程： $\frac{x - 2}{x + 2} - 1 = \frac{16}{x^{2} - 4}$ ．

查看试题解析
23. 解不等式组 ${\begin{matrix} 3 (x - 1) < 5 x + 1 \\ \frac{x - 1}{2} \geq 2 x - 4 \end{matrix}$ ，并把它的解集在数轴上表示出来．再求它的所有的非负整数解．

查看试题解析
24. 先化简，再求值： $(\frac{a + 2}{a^{2} - 2 a} + \frac{8}{4 - a^{2}}) \div \frac{a^{2} - 4}{a}$ ，其中a满足方程a²+4a+1=0．

查看试题解析
25. 如图，平行四边形ABCD中，对角线AC，BD交于O，EO⊥AC，

(1)、若△ABE的周长为10cm，求平行四边形ABCD的周长，

(2)、若∠DAB=108°，AE平分∠BAC，试求∠ACB的度数．

查看试题解析
26. 如图，已知四边形ABCD为平行四边形，AE⊥BD于E，CF⊥BD于F．

(1)、求证：BE=DF；

(2)、若 M、N分别为边AD、BC上的点，且DM=BN，试判断四边形MENF的形状（不必说明理由）．

查看试题解析
27. 某校为美化校园，计划对面积为1800m²的区域进行绿化，安排甲、乙两个工程队完成．已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且在独立完成面积为400m²区域的绿化时，甲队比乙队少用4天．

(1)、求甲、乙两工程队每天能完成绿化的面积分别是多少m²？

(2)、若学校每天需付给甲队的绿化费用为0.4万元，乙队为0.25万元，要使这次的绿化总费用不超过8万元，至少应安排甲队工作多少天？

查看试题解析
28. 已知△ABC是等边三角形，D是BC边上的一个动点（点D不与B，C重合）△ADF是以AD为边的等边三角形，过点F作BC的平行线交射线AC于点E，连接BF．

(1)、如图1，求证：△AFB≌△ADC；

(2)、请判断图1中四边形BCEF的形状，并说明理由；

(3)、若D点在BC 边的延长线上，如图2，其它条件不变，请问（2）中结论还成立吗？如果成立，请说明理由．

查看试题解析