福建省漳州市云霄县2019年中考数学一模考试试卷
试卷更新日期:2020-04-15 类型:中考模拟
一、选择题(共10小题,每小题4分,满分40分.每小题只有一个正确的选项,请把正确的选项填涂在答题卡的相应位置)
-
1. 2019的相反数是( )A、 2019 B、﹣2019 C、 D、﹣2.
图中三视图对应的正三棱柱是( )
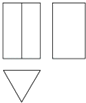 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、(﹣a)3=a3 B、(a2)3=a5 C、a2÷a﹣2=1 D、(﹣2a3)2=4a64. 2018年5月21日,西昌卫星发射中心成功发射探月工程嫦娥四号任务“鹊桥号”中继星,卫星进入近地点高度为200公里、远地点高度为40万公里的预定轨道.将数据40万用科学记数法表示为( )A、4×104 B、4×105 C、4×106 D、0.4×1065. 如图,直线a∥b , 点B在直线b上,且AB⊥BC , ∠1=55°,那么∠2的度数是( )
3. 下列运算正确的是( )A、(﹣a)3=a3 B、(a2)3=a5 C、a2÷a﹣2=1 D、(﹣2a3)2=4a64. 2018年5月21日,西昌卫星发射中心成功发射探月工程嫦娥四号任务“鹊桥号”中继星,卫星进入近地点高度为200公里、远地点高度为40万公里的预定轨道.将数据40万用科学记数法表示为( )A、4×104 B、4×105 C、4×106 D、0.4×1065. 如图,直线a∥b , 点B在直线b上,且AB⊥BC , ∠1=55°,那么∠2的度数是( ) A、20° B、30° C、35° D、50°6. 不等式组 的解集在数轴上表示正确的是( )A、
A、20° B、30° C、35° D、50°6. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、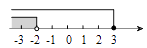 C、
C、 D、
D、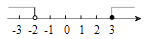 7. 如图,在方格纸中,以AB为一边作△ABP , 使之与△ABC全等,从P1 , P2 , P3 , P4四个点中找出符合条件的点P的概率是( )
7. 如图,在方格纸中,以AB为一边作△ABP , 使之与△ABC全等,从P1 , P2 , P3 , P4四个点中找出符合条件的点P的概率是( )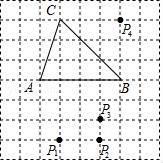 A、 B、 C、 D、18. 1275年我国南宋数学家杨辉提出一个问题:直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步),问阔及长各几步.设阔(宽)为x步,则所列方程正确的是( )A、x(x+12)=864 B、x(x﹣12)=864 C、(x﹣12)(x+12)=864 D、12x=8649. 如图,已知直线y= x﹣3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB . 则△PAB面积的最大值是( )
A、 B、 C、 D、18. 1275年我国南宋数学家杨辉提出一个问题:直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步),问阔及长各几步.设阔(宽)为x步,则所列方程正确的是( )A、x(x+12)=864 B、x(x﹣12)=864 C、(x﹣12)(x+12)=864 D、12x=8649. 如图,已知直线y= x﹣3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB . 则△PAB面积的最大值是( ) A、8 B、12 C、 D、10. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为A(3,0),其部分图象如图所示,下列结论中:①b2<4ac;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;③2a+b=0;④a+b+c<0;⑤当0<x<3时,y随x增大而减小;其中结论正确的个数是( )
A、8 B、12 C、 D、10. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为A(3,0),其部分图象如图所示,下列结论中:①b2<4ac;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;③2a+b=0;④a+b+c<0;⑤当0<x<3时,y随x增大而减小;其中结论正确的个数是( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题(共6小题,每小题4分,满分24分.)
-
11. 计算:(﹣2)0﹣ = .12. 如图,测量试管口径的量具ABC , AB的长为4.5cm , AC被分为60等份.如果试管口DE正好对着量具上20等份处(DE∥AB),那么试管口径DE是cm .
 13. 两组数据m,6,n与1,m,2n,7的平均数都是6,若将这两组数据合并成一组数据,则这组新数据的中位数为 .14. 如图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转36°,点A旋转到A'的位置,则图中阴影部分的面积为(结果保留π).
13. 两组数据m,6,n与1,m,2n,7的平均数都是6,若将这两组数据合并成一组数据,则这组新数据的中位数为 .14. 如图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转36°,点A旋转到A'的位置,则图中阴影部分的面积为(结果保留π).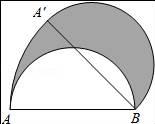 15. 对于任意实数t , 抛物线y=x2+(2﹣t)x+t总经过一个固定的点P , 若反比例函数 经过点P , 则k= .16. 如图,△ABC∽△ADE , ∠BAC=∠DAE=90°,AB=8,AC=6,F是DE的中点,若点E是直线BC上的动点,连接BF , 则BF的最小值是 .
15. 对于任意实数t , 抛物线y=x2+(2﹣t)x+t总经过一个固定的点P , 若反比例函数 经过点P , 则k= .16. 如图,△ABC∽△ADE , ∠BAC=∠DAE=90°,AB=8,AC=6,F是DE的中点,若点E是直线BC上的动点,连接BF , 则BF的最小值是 .
三、解答题(共9题,满分86分.)
-
17. 先化简,再求值: ,其中x=sin45°.18. 已知:如图,∠BAC=∠DAM , AB=AN , ∠B=∠ANM , 求证:AD=AM .
 19. 如图,已知∠ABC , 求作:▱ABCD(要求:①尺规作图,保留作图痕迹,不写作法;②用两种方法作图)
19. 如图,已知∠ABC , 求作:▱ABCD(要求:①尺规作图,保留作图痕迹,不写作法;②用两种方法作图)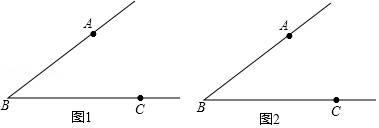 20. 如图,已知△ABC内接于⊙O , AD为直径,点C在劣弧AB上(不与点A , B重合),设∠DAB=α,∠ACB=β,小明同学通过画图和测量得到以下近似数据:
20. 如图,已知△ABC内接于⊙O , AD为直径,点C在劣弧AB上(不与点A , B重合),设∠DAB=α,∠ACB=β,小明同学通过画图和测量得到以下近似数据:α
30°
35°
40°
50°
60°
80°
β
120°
125°
130°
140°
150°
170°
猜想:α关于β的函数表达式,并给出证明.
 21. “校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图.部分信息如下:
21. “校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图.部分信息如下: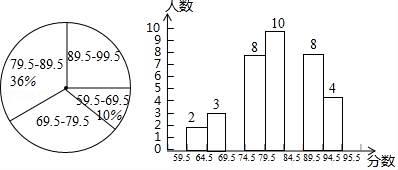 (1)、本次比赛参赛选手共有人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为;(2)、赛前规定,成绩由高到低前40%的参赛选手获奖.某参赛选手的比赛成绩为82分,试判断他能否获奖,并说明理由;(3)、成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率.22. 如图,用48米篱笆围成一个外形为矩形的花园,花园一面利用院墙,中间用一道篱笆间隔成两个小矩形,院墙的长度为20米,平行于院墙的一边长为x米,花园的面积为S平方米.
(1)、本次比赛参赛选手共有人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为;(2)、赛前规定,成绩由高到低前40%的参赛选手获奖.某参赛选手的比赛成绩为82分,试判断他能否获奖,并说明理由;(3)、成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率.22. 如图,用48米篱笆围成一个外形为矩形的花园,花园一面利用院墙,中间用一道篱笆间隔成两个小矩形,院墙的长度为20米,平行于院墙的一边长为x米,花园的面积为S平方米. (1)、求S与x之间的函数关系式;(2)、问花园面积可以达到180平方米吗?如果能,花园的长和宽各是多少?如果不能,请说明理由.23. 已知点P(m , n)和直线y=kx+b , 则点P到直线y=kx+b的距离可用公式d= 计算.
(1)、求S与x之间的函数关系式;(2)、问花园面积可以达到180平方米吗?如果能,花园的长和宽各是多少?如果不能,请说明理由.23. 已知点P(m , n)和直线y=kx+b , 则点P到直线y=kx+b的距离可用公式d= 计算.例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为d= .
根据以上材料,解答下列问题:
(1)、直接写出点P(1,1)到直线y=﹣2x+4的距离d=;(2)、已知直线y=﹣2x+4与y=﹣2x﹣5平行,求这两条直线之间的距离.(3)、已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线 的位置关系并说明理由.24. 【问题情境】(1)、古希腊著名数学家欧几里得在《几何原本》提出了射影定理,又称“欧几里德定理”:在直角三角形中,斜边上的高是两条直角边在斜边射影的比例中项,每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项.射影定理是数学图形计算的重要定理.其符号语言是:如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB , 垂足为D , 则:(1)CD2=AD•BD , (2)AC2=AB•AD , (3)BC2=AB•BD;请你证明定理中的结论(2)BC2=AB•BD .

【结论运用】
(2)、如图2,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE , 垂足为F , 连接OF ,①求证:△BOF∽△BED;
②若BE=2 ,求OF的长.
25. 如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点D , 点B的坐标为(3,0),顶点C的坐标为(1,4).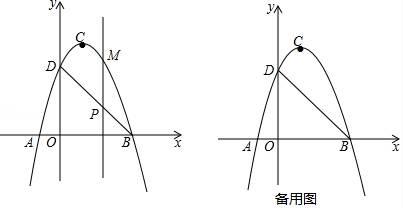 (1)、求二次函数的解析式和直线BD的解析式;(2)、点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M , 当点P在第一象限时,求线段PM长度的最大值;(3)、在抛物线上是否存在异于B、D的点Q , 使△BDQ中BD边上的高为2 ?若存在求出点Q的坐标;若不存在请说明理由.
(1)、求二次函数的解析式和直线BD的解析式;(2)、点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M , 当点P在第一象限时,求线段PM长度的最大值;(3)、在抛物线上是否存在异于B、D的点Q , 使△BDQ中BD边上的高为2 ?若存在求出点Q的坐标;若不存在请说明理由.