福建省三明市2019年中考数学一模考试试卷
试卷更新日期:2020-04-15 类型:中考模拟
一、选择题(共10题,每题4分,满分40分.)
-
1. 下列计算结果等于﹣1的是( )A、﹣1+2 B、(﹣1)0 C、﹣12 D、(﹣1)﹣22. 第十六届海峡交易会对接合同项目2049项,总投资682亿元.将682亿用科学记数法表示为( )A、0.682×1011 B、6.82×1010 C、6.82×109 D、682×1083. 如图所示的几何体左视图是( )
 A、
A、 B、
B、 C、
C、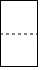 D、
D、 4. 一个不透明的袋子中只装有4个黄球,它们除颜色外完全相同,从中随机摸出一个球.下列说法正确的是( )A、摸到红球的概率是 B、摸到红球是不可能事件 C、摸到红球是随机事件 D、摸到红球是必然事件5. 如图,已知DE为△ABC的中位线,△ADE的面积为3,则四边形DECB的面积为( )
4. 一个不透明的袋子中只装有4个黄球,它们除颜色外完全相同,从中随机摸出一个球.下列说法正确的是( )A、摸到红球的概率是 B、摸到红球是不可能事件 C、摸到红球是随机事件 D、摸到红球是必然事件5. 如图,已知DE为△ABC的中位线,△ADE的面积为3,则四边形DECB的面积为( ) A、6 B、8 C、9 D、126. 如图,A,B,C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为( )
A、6 B、8 C、9 D、126. 如图,A,B,C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为( )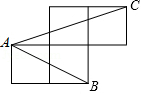 A、 B、1 C、 D、7. 若2n+2n=1,则n的值为( )A、﹣1 B、﹣2 C、0 D、8. 如图,AB , BC是⊙O的两条弦,AO⊥BC , 垂足为D , 若⊙O的半径为5,BC=8,则AB的长为( )
A、 B、1 C、 D、7. 若2n+2n=1,则n的值为( )A、﹣1 B、﹣2 C、0 D、8. 如图,AB , BC是⊙O的两条弦,AO⊥BC , 垂足为D , 若⊙O的半径为5,BC=8,则AB的长为( ) A、8 B、10 C、 D、9. 二次函数y=x2﹣6x+m满足以下条件:当﹣2<x<﹣1时,它的图象位于x轴的下方;当8<x<9时,它的图象位于x轴的上方,则m的值为( )A、27 B、9 C、﹣7 D、﹣1610. 如图,四边形ABCD为正方形,AB=1,把△ABC绕点A逆时针旋转60°得到△AEF , 连接DF , 则DF的长为( )
A、8 B、10 C、 D、9. 二次函数y=x2﹣6x+m满足以下条件:当﹣2<x<﹣1时,它的图象位于x轴的下方;当8<x<9时,它的图象位于x轴的上方,则m的值为( )A、27 B、9 C、﹣7 D、﹣1610. 如图,四边形ABCD为正方形,AB=1,把△ABC绕点A逆时针旋转60°得到△AEF , 连接DF , 则DF的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(共6题,每题4分,满分24分)
-
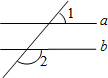
11. 如图,直线a∥b , ∠1=55°,则∠2= .
 12. 某校准备从甲、乙、丙、丁四个科创小组中选出一组,参加区青少年科技创新大赛,表格反映的是各组平时成绩的平均数 (单位:分)及方差S2 , 如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是 .
12. 某校准备从甲、乙、丙、丁四个科创小组中选出一组,参加区青少年科技创新大赛,表格反映的是各组平时成绩的平均数 (单位:分)及方差S2 , 如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是 .甲
乙
丙
丁
7
8
8
7
s2
1
1.2
0.9
1.8
13. 不等式组 的解集是 .14. 程大位是我国珠算发明家.他的著作《直指算法统宗》中记载了一个数学问题,大意是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.问大、小和尚各有多少人?若设大和尚有x人,小和尚有y人,则可列方程组为 .15. 如图,在矩形ABCD中,AD=2,以点A为圆心,AD长为半径画弧,交BC边于点E , 若E恰为BC的中点,则图中阴影部分的面积为 .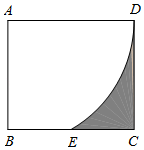 16. 如图,在直角坐标系中,四边形OABC为菱形,OA在x轴的正半轴上,∠AOC=60°,过点C的反比例函数 的图象与AB交于点D , 则△COD的面积为 .
16. 如图,在直角坐标系中,四边形OABC为菱形,OA在x轴的正半轴上,∠AOC=60°,过点C的反比例函数 的图象与AB交于点D , 则△COD的面积为 .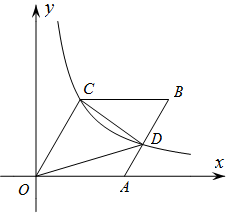
三、解答题(共9题,满分86分.请将解答过程写在答题卡的相应位置,解答应写出文字说明、证明过程或演算步骤.)
-
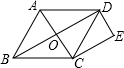
17. 先化简,再求值: ,其中 .18. 菱形ABCD的对角线交于O点,DE∥AC , CE∥BD , 求证:四边形OCED是矩形.
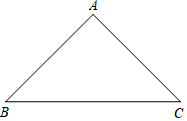
 19. 在平面直角坐标系中,直线l经过点A(﹣1,﹣4)和B(1,0),求直线l的函数表达式.20. 如图,△ABC中,∠A=90°,AB=AC .
19. 在平面直角坐标系中,直线l经过点A(﹣1,﹣4)和B(1,0),求直线l的函数表达式.20. 如图,△ABC中,∠A=90°,AB=AC .(Ⅰ)请用尺规作图的方法在边AC上确定点P , 使得点P到边BC的距离等于PA的长;(保留作图痕迹,不写作法)
(Ⅱ)在(Ⅰ)的条件下,求证:BC=AB+AP .
 21. 某景区的水上乐园有一批4人座的自划船,每艘可供1至4位游客乘坐游湖,因景区加大宣传,预计今年游客将会增加,水上乐园的工作人员随机抽取了去年某天中出租的100艘次4人自划船,统计了每艘船的乘坐人数,制成了如下统计图.
21. 某景区的水上乐园有一批4人座的自划船,每艘可供1至4位游客乘坐游湖,因景区加大宣传,预计今年游客将会增加,水上乐园的工作人员随机抽取了去年某天中出租的100艘次4人自划船,统计了每艘船的乘坐人数,制成了如下统计图.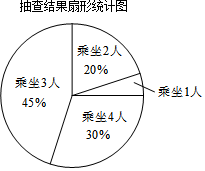 (1)、扇形统计图中,“乘坐1人”所对应的圆心角度数为;(2)、所抽取的自划船每艘乘坐人数的中位数是;(3)、若每天将增加游客300人,那么每天需多安排多少艘次4人座的自划船才能满足需求?22. 惠好商场用24000元购进某种玩具进行销售,由于深受顾客喜爱,很快脱销,惠好商场又用50000元购进这种玩具,所购数量是第一次购进数量的2倍,但每套进价比第一次多了10元.
(1)、扇形统计图中,“乘坐1人”所对应的圆心角度数为;(2)、所抽取的自划船每艘乘坐人数的中位数是;(3)、若每天将增加游客300人,那么每天需多安排多少艘次4人座的自划船才能满足需求?22. 惠好商场用24000元购进某种玩具进行销售,由于深受顾客喜爱,很快脱销,惠好商场又用50000元购进这种玩具,所购数量是第一次购进数量的2倍,但每套进价比第一次多了10元.(Ⅰ)惠好商场第一次购进这种玩具多少套?
(Ⅱ)惠好商场以每套300元的价格销售这种玩具,当第二次购进的玩具售出 时,出现了滞销,商场决定降价促销,若要使第二次购进的玩具销售利润率不低于12%,剩余的玩具每套售价至少要多少元?
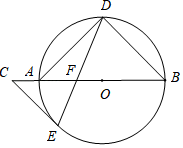
23. 如图,AB是⊙O的直径,点D , E在⊙O上,∠B=2∠ADE , 点C在BA的延长线上.(Ⅰ)若∠C=∠DAB , 求证:CE是⊙O的切线;
(Ⅱ)若OF=2,AF=3,求EF的长.
 24. 如图,在△ABC中,点P是BC边上的动点,点M是AP的中点,PD⊥AB , 垂足为D , PE⊥AC , 垂足为E , 连接MD , ME .
24. 如图,在△ABC中,点P是BC边上的动点,点M是AP的中点,PD⊥AB , 垂足为D , PE⊥AC , 垂足为E , 连接MD , ME .(Ⅰ)求证:∠DME=2∠BAC;
(Ⅱ)若∠B=45°,∠C=75°,AB= ,连接DE , 求△MDE周长的最小值.
 25. 已知二次函数y1=mx2﹣nx﹣m+n(m>0).
25. 已知二次函数y1=mx2﹣nx﹣m+n(m>0).(Ⅰ)求证:该函数图象与x轴必有交点;
(Ⅱ)若m﹣n=3,
(ⅰ)当﹣m≤x<1时,二次函数的最大值小于0,求m的取值范围;
(ⅱ)点A(p , q)为函数y2=|mx2﹣nx﹣m+n|图象上的动点,当﹣4<p<﹣1时,点A在直线y=﹣x+4的上方,求m的取值范围.