福建省三明市梅列区、永安区2019年中考数学一模考试试卷
试卷更新日期:2020-04-15 类型:中考模拟
一、选择题(本题共10小题,每小题4分,满分40分.在每小题给出的四个选中,只有一项是符合题目要求的)
-
1. |﹣5|的值是( )A、5 B、﹣5 C、 D、-2. 已知某新型感冒病毒的直径约为0.000000823米,将0.000000823用科学记数法表示为( )A、8.23×10﹣6 B、8.23×10﹣7 C、8.23×106 D、8.23×1073. 下列运算正确的是( )A、a2+a3=a5 B、a2÷a2=a C、3a2•a3=3a5 D、(3a2)3=9a64. 如图所示的几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,直线AB∥CD , 则下列结论正确的是( )
5. 如图,直线AB∥CD , 则下列结论正确的是( )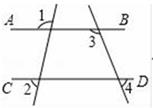 A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠3+∠4=180°6. 洛阳某中学“研究学习小组”的同学们进行了社会实践活动,其中一个小组的同学调查了30户家庭某月的用水量,如表所示:
A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠3+∠4=180°6. 洛阳某中学“研究学习小组”的同学们进行了社会实践活动,其中一个小组的同学调查了30户家庭某月的用水量,如表所示:用水量(吨)
15
20
25
30
41
户数
3
6
7
9
5
则这30户家庭用水量的众数和中位数分别是( )
A、25,27 B、25,25 C、30,27 D、30,257. 不等式组 的解集在数轴表示,正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,AB是⊙O的直径,C是⊙O上一点(A、E除外),∠AOD=132°,则∠C的度数是( )
8. 如图,AB是⊙O的直径,C是⊙O上一点(A、E除外),∠AOD=132°,则∠C的度数是( ) A、68° B、48° C、34° D、24°9. 用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是( )
A、68° B、48° C、34° D、24°9. 用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是( )
A、 B、
B、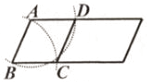 C、
C、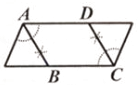 D、
D、 10. 如图,在平面直角坐标系中,矩形ABCD的顶点B在原点,点A、C在坐标轴上,点D的坐标为(6,4),E为CD的中点,点P、Q为BC边上两个动点,且PQ=2,要使四边形APQE的周长最小,则点P的坐示应为( )
10. 如图,在平面直角坐标系中,矩形ABCD的顶点B在原点,点A、C在坐标轴上,点D的坐标为(6,4),E为CD的中点,点P、Q为BC边上两个动点,且PQ=2,要使四边形APQE的周长最小,则点P的坐示应为( ) A、(2,0) B、 C、(4,0) D、
A、(2,0) B、 C、(4,0) D、二、填空题(本题共6小题,每小题4分,满分24分)
-
11. 的相反数是 , 的倒数是 .12. 在0,- ,2, , 中任取一个数,取到无理数的概率是 .13. 若代数式 和 的值相等,则x= .14. 我国南宋数学家杨辉曾提出这样一个问题:“直田积(矩形面积),八百六十四(平方步),只云阔(宽)不及长一十二步(宽比长少12步),问阔及长各几步.”如果设矩形田地的长为x步,那么根据题意列出的方程为.15. 如图:在△ABC中,CE平分∠ACB , CF平分∠ACD , 且EF∥BC交AC于M , 若CM=5,则CE2+CF2= .
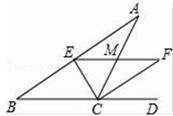 16. 如图,在菱形ABCD中,∠ABC=60°,AB=5,点E是AD边上的动点,过点B作直线CE的垂线,垂足为F , 当点E从点A运动到点D时,点F的运动路径长为 .
16. 如图,在菱形ABCD中,∠ABC=60°,AB=5,点E是AD边上的动点,过点B作直线CE的垂线,垂足为F , 当点E从点A运动到点D时,点F的运动路径长为 .
三、解答题(本題共9小题,共86分)
-
17. 计算: ﹣3tan30°+(π﹣4)0﹣( )﹣1 .18. 如图,AE∥FD , AE=FD , B、C在直线EF上,且BE=CF ,
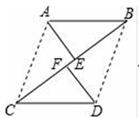 (1)、求证:△ABE≌△DCF;(2)、试证明:以A、B、D、C为顶点的四边形是平行四边形.19. 先化简,再求值: ,其中a=﹣1.20. 某中学组织学生参加交通安全知识网络测试活动,小华对九年(8)班全体学生的测试成绩进行了统计,并将成绩分为四个等级:优秀、良好、一般、不合格,绘制成如下的统计图(不完整),请你根据图中所给的信息解答下列问题:
(1)、求证:△ABE≌△DCF;(2)、试证明:以A、B、D、C为顶点的四边形是平行四边形.19. 先化简,再求值: ,其中a=﹣1.20. 某中学组织学生参加交通安全知识网络测试活动,小华对九年(8)班全体学生的测试成绩进行了统计,并将成绩分为四个等级:优秀、良好、一般、不合格,绘制成如下的统计图(不完整),请你根据图中所给的信息解答下列问题: (1)、九年(8)班有名学生,并把折线统计图补充完整;(2)、已知该市共有11000名中学生参加了这次交通安全知识测试,请你根据该班成绩估计该市在这次测试中成绩为优秀的人数;(3)、小王查了该市教育网站发现,全市参加本次测试的学生中,成绩为优秀的有5200人,请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因.21. 我市公交总公司为节约资源同时惠及民生,拟对一些乘客数量较少的路线换成中巴车,该公司计划购买10台中巴车,现有甲、乙两种型号,已知购买一台甲型车比购买一台乙型车少10万元,购买3台甲型车比购买2台乙型车多30万元.(1)、问购买一台甲型车和一台乙型车分别需要多少万元?(2)、经了解,每台甲型车每年节省2.5万元,每台乙型车每年节省2.1万元,若要使购买的这批中巴车每年至少能节省21.8万,则购买甲型车至少需至少多少台?22. 某课桌生产厂家研究发现,倾斜12°﹣24°的桌面有利于学生保持躯体自然姿势,根据这一研究,厂家决定将水平桌面做成可调节角度的桌面,新桌面的设计图如图1所示,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD , AC=30cm .
(1)、九年(8)班有名学生,并把折线统计图补充完整;(2)、已知该市共有11000名中学生参加了这次交通安全知识测试,请你根据该班成绩估计该市在这次测试中成绩为优秀的人数;(3)、小王查了该市教育网站发现,全市参加本次测试的学生中,成绩为优秀的有5200人,请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因.21. 我市公交总公司为节约资源同时惠及民生,拟对一些乘客数量较少的路线换成中巴车,该公司计划购买10台中巴车,现有甲、乙两种型号,已知购买一台甲型车比购买一台乙型车少10万元,购买3台甲型车比购买2台乙型车多30万元.(1)、问购买一台甲型车和一台乙型车分别需要多少万元?(2)、经了解,每台甲型车每年节省2.5万元,每台乙型车每年节省2.1万元,若要使购买的这批中巴车每年至少能节省21.8万,则购买甲型车至少需至少多少台?22. 某课桌生产厂家研究发现,倾斜12°﹣24°的桌面有利于学生保持躯体自然姿势,根据这一研究,厂家决定将水平桌面做成可调节角度的桌面,新桌面的设计图如图1所示,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD , AC=30cm . (1)、如图2,当∠BAC=24°时,CD⊥AB , 求支撑臂CD的长;(2)、如图3,若CD长是10cm , 当∠BAC=12°时,求A、D两点间的距离.(参考数据:sin24°≈0.40,cos24°≈0.91,sin12°≈0.20,cos12°≈0.98)23. 已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)、如图2,当∠BAC=24°时,CD⊥AB , 求支撑臂CD的长;(2)、如图3,若CD长是10cm , 当∠BAC=12°时,求A、D两点间的距离.(参考数据:sin24°≈0.40,cos24°≈0.91,sin12°≈0.20,cos12°≈0.98)23. 已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E. (1)、求证:点D是AB的中点;(2)、判断DE与⊙O的位置关系,并证明你的结论;(3)、若⊙O的直径为10,tanB=3,求DE的长.24. 如图1,在矩形纸片ABCD中,AB=12cm , AD=20cm , 折叠纸片使B点落在边AD上的E处,折痕为PQ , 过点E作EF∥AB交PQ于F , 连接BF .
(1)、求证:点D是AB的中点;(2)、判断DE与⊙O的位置关系,并证明你的结论;(3)、若⊙O的直径为10,tanB=3,求DE的长.24. 如图1,在矩形纸片ABCD中,AB=12cm , AD=20cm , 折叠纸片使B点落在边AD上的E处,折痕为PQ , 过点E作EF∥AB交PQ于F , 连接BF . (1)、求证:四边形BFEP为菱形;(2)、当点E在AD边上移动时,折痕的端点P、Q也随之移动;
(1)、求证:四边形BFEP为菱形;(2)、当点E在AD边上移动时,折痕的端点P、Q也随之移动;①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.
25. 已知二次函数y=x2+(2m﹣2)x+m2﹣2m﹣3(m是常数)的图象与x轴交于A , B两点(点A在点B的左边). (1)、如果二次函数的图象经过原点.
(1)、如果二次函数的图象经过原点.①求m的值;
②若m<0,点C是一次函数y=﹣x+b(b>0)图象上的一点,且∠ACB=90°,求b的取值范围;
(2)、当﹣3≤x≤2时,函数的最大值为5,求m的值.