福建省莆田市2019年中考数学4月模拟考试试卷

试卷更新日期：2020-04-15 类型：中考模拟

进入出卷网下载

一、选择：本大题共10小题，每小题4分，共40分。

1. ﹣2的相反数是（）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
2. 如图所示，该几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列选项中，可以用来证明命题“若a是实数，则|a|＞0”是假命题的反例是（）

A、a＝﹣1 B、a＝0 C、a＝1 D、a＝2

查看试题解析
4. 如图，将“笑脸”图标向右平移4个单位，再向下平移2个单位，点P的对应点P'的坐标是（）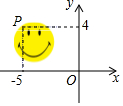

A、（﹣1，6） B、（﹣9，6） C、（﹣1，2） D、（﹣9，2）

查看试题解析
5. 长度分别为 $2$ ， $7$ ， $x$ 的三条线段能组成一个三角形， $x$ 的值可以是（）

A、 $4$ B、 $5$ C、 $6$ D、 $9$

查看试题解析
6. 若二次函数y＝ax²﹣3x+7﹣5x²在坐标平面上的图形有最低点，则a的值可以是（）

A、a＝0 B、a＝2 C、a＝4 D、a＝6

查看试题解析
7. 投掷两枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数，则下列事件为随机事件的是（）

A、两枚骰子向上一面的点数之和大于1 B、两枚骰子向上一面的点数之和等于1 C、两枚骰子向上一面的点数之和大于12 D、两枚骰子向上一面的点数之和等于12

查看试题解析
8. 如图，已知△ABC和△PBD都是正方形网格上的格点三角形（顶点为网格线的交点），要使△ABC∽△PBD ，则点P的位置应落在（）

A、点P₁上 B、点P₂上 C、点P₃上 D、点P₄上

查看试题解析
9. 某数学研究性学习小组制作了如下的三角函数计算图尺：在半径为1的半圆形量角器中，画一个直径为10的圆，把刻度尺CA的0刻度固定在半圆的圆心O处，刻度尺可以绕点O旋转．从图中所示的图尺可读出sin∠AOB的值是（）

A、 $\frac{5}{8}$ B、 $\frac{7}{8}$ C、 $\frac{7}{10}$ D、 $\frac{4}{5}$

查看试题解析
10. 点A（x ， y）为平面直角坐标系内一点，其中x ， y满足3，x+2，y﹣4中的两个数相等，则所有的点A组成的图形为（）

A、一个点 B、两条相交的直线 C、一个三角 D、相交于一点的三条直线

查看试题解析

二、填空题：本大题共6小题，每小题4分，共24分.

11. 计算：cos60°+（ $\frac{1}{2}$ ）⁰＝

查看试题解析
12. 已知关于x的方程x²﹣3x+m=0的一个根是1，则m= ．

查看试题解析
13.
七（1）班举行投篮比赛，每人投5球．如图是全班学生投进球数的扇形统计图，则投进球数的众数是．

查看试题解析
14. 如图，在矩形ABCD中，AD＝3，将矩形ABCD绕点A逆时针旋转，得到矩形AEFG ，点B的对应点E落在CD上，且DE＝EF ，则AB的长为．

查看试题解析
15. 等宽曲线是这样的一种几何图形，它们在任何方向上的直径（或称宽度）都是相等的．如图，分别以等边△ABC的三个顶点为圆心，边长为半径画弧则弧AB ，弧BC弧AC组成的封闭图形就是“莱洛三角形”．莱洛三角形是“等宽曲线”，用莱洛三角形做横断面的滚子，能使载重物水平地移动而不至于上下颠簸．诺AB＝3，则此“莱诺三角形”的周长为．

查看试题解析
16. 如图，含30°的直角三角板ABC（其中∠ABC＝90°）的三个顶点均在反比例函数y＝ $\frac{1}{x}$ 的图象上，且斜边AC经过原点O ，则直角三角板ABC的面积为．

查看试题解析

三、解答题：本大题共9小题，共86分.

17. 解方程： $\frac{3}{x - 1}$ ﹣ $\frac{2}{x}$ ＝0．

查看试题解析
18. 如图，△ABC中，点D ， E分别是边BC ， AC的中点，连接DE ， AD ，点F在BA的延长线上，且AF＝ $\frac{1}{2}$ AB ，连接EF ，判断四边形ADEF的形状，并加以证明．

查看试题解析
19. 化简求值： $\frac{1}{a - 1}$ ﹣ $\frac{1}{a^{2} + a}$ ÷ $\frac{a^{2} - 1}{a^{2} + 2 a + 1}$ ，其中a＝ $\sqrt{3}$ ．

查看试题解析
20. 如图，O为正方形ABCD对角线上一点，以O为圆心，OA长为半径的⊙O与BC相切于点M ．

(1)、求证：CD与⊙O相切．

(2)、若正方形ABCD的边长为1，求⊙O的半径．

查看试题解析
21. 问题提出学习了全等三角形的判定方法（“SSS”“SAS”“ASA”“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．

初步思考将问题用符号语言表示为：在△ABC和△DEF中，AC＝DF ， BC＝EF ， ∠ABC＝∠DEF ，然后对∠ABC进行分类，可分为“∠ABC是锐角、直角、钝角”三种情况进行探究．

第一种情况：当∠ABC是锐角时，AB＝DE不一定成立

第二种情况：当∠ABC是直角时，根据“HL”，可得△ABC≌△DEF ，则AB＝DE；

第三种情况，当∠ABC是钝角时，则AB＝DE ．

如图，在△ABC和△DEF中，AC＝DF ， BC＝EF ． ∠ABC＝∠DEF ，且∠ABC是钝角．求证：AB＝DE；

方法归纳化归是一种有效的数学思维方式，一般是将未解决的问题通过变换转化为已解决的问题，观察发现第三种情况可以转化为第二种情况，如图，过点C作CG⊥AB交延长线于点G ．

(1)、在△DEF中用尺规作出DE边上的高FH ，不写作法，保留作图痕迹；

(2)、请你完成（1）中作图的基础上，加以证明AB＝DE ．

查看试题解析

22. 电影公司随机收集了电影的有关数据，经分类整理得到下表

电影类型	第一类	第二类	第三类	第四类	第五类	第六类
电影部数	140	50	300	200	800	510
获得好评的电影部数	56	10	45	50	160	51

(1)、从电影公司收集的电影中随机选取1部，求这部电影是获得好评的第四类电影的概率；

(2)、电影公司为增加投资回报，需在调查前根据经验预估每类电影的好评率（好评率是指：一类电影中获得好评的部数与该类电影的部数的比值），如表所示：

电影类型	第一类	第二类	第三类	第四类	第五类	第六类
好评率	0.5	0.2	0.15	0.15	0.4	0.3

定义统计量S＝ $\frac{1}{n}$ [（ $P_{1}^{'}$ ﹣P₁）²+（ $P_{2}^{'}$ ﹣P₂）²+…+（ $P_{n}^{'}$ ﹣P_n）²]，其中 $P_{i}^{'}$ 为第i类电影的实测好评率，P_i为第i类电影的预估好评率（i＝1，2，…，n）．规定：若S＜0.05，则称该次电影的好评率预估合理，否则为不合理，判断本次电影的好评率预估是否合理．

查看试题解析

23. 如图1是某品牌的一款学生斜挎包，其挎带由单层部分、双层部分和调节扣组成，设单层部分的长度为xcm ，双层部分的长度为ycm ，经测量，得到如下数据：

x（cm）

0

4

6

8

10

．．

120

y（cm）

m

58

57

56

55

n

(1)、如图2，在平面直角坐标系中，以所测得数据中的x为横坐标，以y为纵坐标，描出所表示的点，并用平滑曲线连接，并根据图象猜想求出该函数的解析式；

(2)、若小花要购买一个持带长为125cm的斜持包，该款式的斜挎包是否满足小花的需求？请说明理由．（持带的总长度＝单层部分长度+双层部分长度，其中调节扣的长度忽略不计）

查看试题解析
24. 如图，菱形ABCD中，∠ABC＝60°，E为AB中点，F为BC上一点，G为CD上一点，连接EF ， FG ，且∠BFE＝∠CFG ．

(1)、若G为CD中点时，求证：EF＝FG；

(2)、设x＝ $\frac{F G}{E F}$ ，y＝ $\frac{S_{△ C F G}}{S_{菱形 A B C D}}$ ，求y关于x的函数解析式．

查看试题解析
25. 若抛物线与x轴的两个交点及其顶点构成等边三角形，则称该抛物线为“等边抛物线”

(1)、若对任意m ， n ，点M（m ， n）和点N（﹣m+4，n）恒在“等边抛物线”C₁：y＝ax²+bx上，求抛物线C₁的解析式；

(2)、若抛物线C₂：y＝ax²+bx+c为“等边抛物线“，求b²﹣4ac的值；

(3)、对于“等边抛物线“C₃：y＝x²+bx+c ，当1＜x＜m时，总存在实数b ，使二次函数C₃的图象在一次函数y＝x图象的下方，求m的最大值．

查看试题解析

x（cm）	0	4	6	8	10	．．	120
y（cm）	m	58	57	56	55		n