福建省龙岩市永定区、连城县2019年中考数学5月模拟考试试卷
试卷更新日期:2020-04-15 类型:中考模拟
一、选择题(本题共10小题,每小题4分,共40分)
-
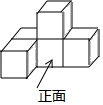
1. 下列实数为无理数的是( )A、﹣5 B、 C、0 D、π2. 如图,这是由5个大小相同的正方体搭成的几何体,该几何体的左视图( )
 A、
A、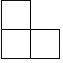 B、
B、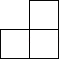 C、
C、 D、
D、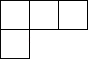 3. 在平面直角坐标系中,点A(1, )绕原点顺时针旋转90°,得到点A',则点A'的坐标为( )A、(﹣ ,1) B、( ,﹣1) C、(﹣1, ) D、(1, )4. 这段时间,一个叫“学习强国”的理论学习平台火了,很多人主动下载、积极打卡,兴起了一股全民学习的热潮.据不完全统计,截止4月2号,华为官方应用市场“学习强国APP”下载量已达8830万次,请将8830万用科学记数法表示为( )A、0.883×109 B、8.83×108 C、8.83×107 D、88.3×1065. 下列运算正确的是( )A、7a﹣a=6 B、a2•a3=a5 C、(a3)3=a6 D、(ab)4=ab46. 不等式组 的解集在数轴上表示为( )A、
3. 在平面直角坐标系中,点A(1, )绕原点顺时针旋转90°,得到点A',则点A'的坐标为( )A、(﹣ ,1) B、( ,﹣1) C、(﹣1, ) D、(1, )4. 这段时间,一个叫“学习强国”的理论学习平台火了,很多人主动下载、积极打卡,兴起了一股全民学习的热潮.据不完全统计,截止4月2号,华为官方应用市场“学习强国APP”下载量已达8830万次,请将8830万用科学记数法表示为( )A、0.883×109 B、8.83×108 C、8.83×107 D、88.3×1065. 下列运算正确的是( )A、7a﹣a=6 B、a2•a3=a5 C、(a3)3=a6 D、(ab)4=ab46. 不等式组 的解集在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、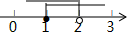 7. 为迎接中考体育加试,小刚和小亮分别统计了自己最近10次跳绳成绩,下列统计中能用来比较两人成绩稳定程度的是( )A、平均数 B、中位数 C、众数 D、方差8. 《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆柱形木材的直径是多少?”
7. 为迎接中考体育加试,小刚和小亮分别统计了自己最近10次跳绳成绩,下列统计中能用来比较两人成绩稳定程度的是( )A、平均数 B、中位数 C、众数 D、方差8. 《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆柱形木材的直径是多少?”如图所示,请根据所学知识计算:圆柱形木材的直径AC是( )
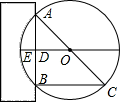 A、13寸 B、20寸 C、26寸 D、28寸9. 如图,平行于x轴的直线与函数y= (k1>0,x>0),y= (k2>0,x>0)的图象分别相交于A , B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为4,则k1﹣k2的值为( )
A、13寸 B、20寸 C、26寸 D、28寸9. 如图,平行于x轴的直线与函数y= (k1>0,x>0),y= (k2>0,x>0)的图象分别相交于A , B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为4,则k1﹣k2的值为( ) A、8 B、﹣8 C、4 D、﹣410. 在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )
A、8 B、﹣8 C、4 D、﹣410. 在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )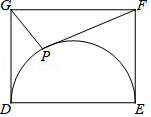 A、 B、 C、34 D、10
A、 B、 C、34 D、10二、填空题(本题共6小题,每小题4分,共24分)
-
11. 已知a是x2﹣3x+1=0的根,则2a2﹣6a= .12. 圆锥的底面半径为3cm , 母线长为5cm , 则它的侧面积为 .13. 一个暗箱中放有除颜色外其他完全相同的n个红球,18个黄球,9个白球,现将球搅匀后,任意摸出1个球记下颜色,再放回暗箱,通过大量重复试验后发现,摸到黄球的频率稳定在30%附近,由此可以估算的n值是 .14. 如图,AB、AC都是圆O的弦,OM⊥AB , ON⊥AC , 垂足分别为M、N , 如果MN=3,那么BC= .
 15. 小卖部从批发市场购进一批李子,在销售了部分李子之后,余下的每千克降价3元,直至全部售完.销售金额(元)与李子销售量(千克)之间的关系如图所示.若销售这批李子一共赢利220元,那么这批李子的进价是元.
15. 小卖部从批发市场购进一批李子,在销售了部分李子之后,余下的每千克降价3元,直至全部售完.销售金额(元)与李子销售量(千克)之间的关系如图所示.若销售这批李子一共赢利220元,那么这批李子的进价是元.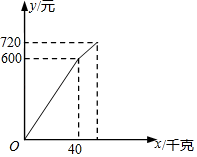 16. 如图,在矩形ABCD中,AB=3,CB=2,点E为线段AB上的动点,将△CBE沿CE折叠,使点B落在矩形内点F处,下列结论正确的是(写出所有符合题意结论的序号)
16. 如图,在矩形ABCD中,AB=3,CB=2,点E为线段AB上的动点,将△CBE沿CE折叠,使点B落在矩形内点F处,下列结论正确的是(写出所有符合题意结论的序号)①当E为线段AB中点时,AF∥CE;
②当E为线段AB中点时,AF= ;
③当A、F、C三点共线时,AE= ;
④当A、F、C三点共线时,△CEF≌△AEF .

三、解答题:(本题共9小题,共86分)
-
17. 计算:18. 先化简 ÷( ﹣x+1),然后从﹣ <x< 的范围内选取一个合适的整数作为x的值代入求值.19. 如图,已知∠MON , 点B , C分别在射线OM , ON上,且OB=OC .
 (1)、用直尺和圆规作出∠MON的角平分线OP , 在射线OP上取一点A , 分别连接AB、AC(只需保留作图痕迹,不要求写作法).(2)、在(1)的条件下求证:AB=AC .20. 某旅游团到永定土楼观光,计划购买A型、B型两种型号的土楼模型.若购买8个A型土楼模型和5个B型土楼模型需用1540元;若购买4个A型土楼模型和6个B型土楼模型需用1120元.求A , B两种型号土楼模型的单价分别是多少元.21. 根据最新公布的福建高考改革方案,从2021年开始我省高考将实行“3+1+2”模式.“3“指的是语文、数学、外语三科为必考科目,不分文理科,由全国统一命题;“1+2“为高中学业水平选择性考试,其中“1“为在物理、历史2科中选择1科;“2“为在思想政治、地理、化学、生物4科中选择2科.现对该校某班选科情况进行调查,对调查结果进行了分析统计,并制作了两幅不完整的统计图.
(1)、用直尺和圆规作出∠MON的角平分线OP , 在射线OP上取一点A , 分别连接AB、AC(只需保留作图痕迹,不要求写作法).(2)、在(1)的条件下求证:AB=AC .20. 某旅游团到永定土楼观光,计划购买A型、B型两种型号的土楼模型.若购买8个A型土楼模型和5个B型土楼模型需用1540元;若购买4个A型土楼模型和6个B型土楼模型需用1120元.求A , B两种型号土楼模型的单价分别是多少元.21. 根据最新公布的福建高考改革方案,从2021年开始我省高考将实行“3+1+2”模式.“3“指的是语文、数学、外语三科为必考科目,不分文理科,由全国统一命题;“1+2“为高中学业水平选择性考试,其中“1“为在物理、历史2科中选择1科;“2“为在思想政治、地理、化学、生物4科中选择2科.现对该校某班选科情况进行调查,对调查结果进行了分析统计,并制作了两幅不完整的统计图.
请根据以上信息,完成下列问题:
(1)、该班共有学生人;(2)、请将条形统计图补充完整;(3)、该班某同学物理成绩特别优异,已经从物理、历史学科中选定物理,还需从余下思想政治、地理、化学、生物(分别记为A、B、C、D)4门科目中任意选择两门,请用列表或画树状图的方法,求出该同学恰好选中化学、生物两科的概率.22. 如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD . (1)、求证:CD是⊙O的切线;(2)、过点B作⊙O的切线交CD的延长线于点E , 若BC=4,tan∠ABD= ,求BE的长.23. 知识背景:
(1)、求证:CD是⊙O的切线;(2)、过点B作⊙O的切线交CD的延长线于点E , 若BC=4,tan∠ABD= ,求BE的长.23. 知识背景:当a>0且x>0时,因为 ,所以x﹣2 ≥0,
从而 (当 = ,即x= 时取等号).
设函数y=x+ (x>0,a>0),由上述结论可知:当x= 时,该函数有最小值2 .
应用举例
已知函数为y1=x(x>0)与函数y2= (x>0),则当x= 时,y1+y2=x+ 有最小值为2 .
解决问题
(1)、已知函数为y1=x﹣1(x>1)与函数y2=(x﹣1)2+9(x>1),当x取何值时, 有最小值?最小值是多少?(2)、已知某设备租赁使用成本包含以下三部分:一是设备的安装调试费用,共490元;二是设备的租赁使用费用,每天200元;三是设备的折旧费用,它与使用天数的平方成正比,比例系数为0.001.若设该设备的租赁使用天数为x天,则当x取何值时,该设备平均每天的租赁使用成本最低?最低是多少元?24. 定义:点P是四边形ABCD内一点,若三角形△PAB , △PBC , △PCD , △PDA均为等腰三角形,则称点P是四边形ABCD的一个“准中心”,如,正方形的中心就是它的一个“准中心”. (1)、如图,已知点P是正方形ABCD内的一点,且∠PBC=∠PCB=60°,证明点P是正四边形ABCD的一个“准中心”;(2)、填空:正方形ABCD共有个“准中心”;(3)、已知∠BAD=60°,AB=AD=6,点C是∠BAD平分线上的动点,问在四边形ABCD的对角线AC上最多存在几个“准中心”点P(自行画出示意图),并求出每个“准中心”点P对应线段AC的长(精确到个位).25. 在平面直角坐标系中,点O(0,0),点A(1,0).已知抛物线y=x2+mx﹣2m(m是常数),顶点为P .
(1)、如图,已知点P是正方形ABCD内的一点,且∠PBC=∠PCB=60°,证明点P是正四边形ABCD的一个“准中心”;(2)、填空:正方形ABCD共有个“准中心”;(3)、已知∠BAD=60°,AB=AD=6,点C是∠BAD平分线上的动点,问在四边形ABCD的对角线AC上最多存在几个“准中心”点P(自行画出示意图),并求出每个“准中心”点P对应线段AC的长(精确到个位).25. 在平面直角坐标系中,点O(0,0),点A(1,0).已知抛物线y=x2+mx﹣2m(m是常数),顶点为P .(Ⅰ)当抛物线经过点A时,求顶点P的坐标;
(Ⅱ)若点P在x轴下方,当∠AOP=45°时,若函数值y>0,求对应自变量x的取值范围;
(Ⅲ)无论m取何值,该抛物线都经过定点H . 当∠AHP=45°时,求抛物线的解析式.