福建省福州市2019年中考数学二模考试试卷
试卷更新日期：2020-04-15 类型：中考模拟
一、选择题：本题共10小题，每小题4分，共40分
-
1. 下列天气预报的图标中既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
2. 地球绕太阳公转的速度约是110000千米/时，将110000用科学记数法表示为（ ）A、11×104 B、1.1×104 C、1.1×105 D、0.11×1063. 已知△ABC∽△DEF ， 若面积比为4：9，则它们对应高的比是（ ）A、4：9 B、16：81 C、3：5 D、2：34. 若正数x的平方等于7，则下列对x的估算正确的是（ ）A、1＜x＜2 B、2＜x＜3 C、3＜x＜4 D、4＜x＜55. 已知a∥b ， 将等腰直角三角形ABC按如图所示的方式放置，其中锐角顶点B ， 直角顶点C分别落在直线a ， b上，若∠1＝15°，则∠2的度数是（ ）
A、15° B、22.5° C、30° D、45°6. 下列各式的运算或变形中，用到分配律的是（ ）A、2 ×3 ＝6 B、（ab）2＝a2b2 C、由x+2＝5得x＝5﹣2 D、3a+2a＝5a7. 袋中装有除颜色外完全相同的a个白球，b个红球，c个黄球，则任意摸出一个球是红球的概率是（ ）A、 B、 C、 D、8. 如图，等边三角形ABC边长为5、D、E分别是边AB、AC上的点，将△ADE沿DE折叠，点A恰好落在BC边上的点F处，若BF＝2，则BD的长是（ ）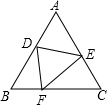
A、 B、 C、3 D、29. 已知Rt△ABC ， ∠ACB＝90°，AC＝3，BC＝4，AD平分∠BAC ， 则点B到射线AD的距离是（ ）A、2 B、 C、 D、310. 一套数学题集共有100道题，甲、乙和丙三人分别作答，每道题至少有一人解对，且每人都解对了其中的60道．如果将其中只有1人解对的题称作难题，2人解对的题称作中档题，3人都解对的题称作容易题，那么下列判断一定正确的是（ ）A、容易题和中档题共60道 B、难题比容易题多20道 C、难题比中档题多10道 D、中档题比容易题多15道二、填空题：本题共6小题，每小题4分，共24分
-
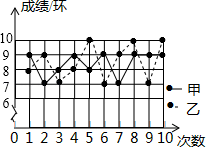
11. 分解因式：m3﹣4m= ．12. 若某几何体从某个方向观察得到的视图是正方形，则这个几何体可以是 ．13. 如图是甲、乙两射击运动员10次射击成绩的折线统计图，则这10次射击成绩更稳定的运动员是 ．
14. 若分式 的值是负整数，则整数m的值是 ．15. 在平面直角坐标系中，以原点为圆心，5为半径的⊙O与直线y＝kx+2k+3（k≠0）交于A ， B两点，则弦AB长的最小值是 ．16. 如图，在平面直角坐标系中，O为原点，点A在第一象限，点B是x轴正半轴上一点，∠OAB＝45°，双曲线y＝ 过点A ， 交AB于点C ， 连接OC ， 若OC⊥AB ， 则tan∠ABO的值是 ．
三、解答题：本题共9小题，共86分
-
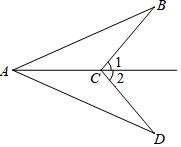
17. 计算：|﹣3|+ •tan30°﹣（3.14﹣π）018. 如图，已知∠1＝∠2，∠B＝∠D ， 求证：CB＝CD ．
19. 先化简，再求值：（1﹣ ）÷ ，其中x＝ +1．20. 如图，在Rt△ABC中，∠ACB＝90°，BD平分∠ABC ． 求作⊙O ， 使得点O在边AB上，且⊙O经过B、D两点；并证明AC与⊙O相切．（尺规作图，保留作图痕迹，不写作法）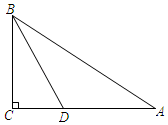
21. 如图，将△ABC沿射线BC平移得到△A'B'C'，使得点A'落在∠ABC的平分线BD上，连接AA'、AC'．
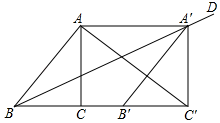(1)、判断四边形ABB'A'的形状，并证明；(2)、在△ABC中，AB＝6，BC＝4，若AC′⊥A'B'，求四边形ABB'A'的面积．22. 为了解某校九年级学生体能训练情况，该年级在3月份进行了一次体育测试，决定对本次测试的成绩进行抽样分析．已知九年级共有学生480人，请按要求回答下列问题：(1)、把全年级同学的测试成绩分别写在没有明显差别的小纸片上，揉成小球，放到一个不透明的袋子中，充分搅拌后，随意抽取30个，展开小球，记录这30张纸片中所写的成绩得到一个样本，你觉得上面的抽取过程是简单随机抽样吗？答：（填“是”或“不是”）
(2)、下表是用简单随机抽样方法抽取的30名同学的体育测试成绩（单位：分）：59
69
77
73
72
62
79
78
66
81
85
84
83
84
86
87
88
85
86
89
90
97
91
98
90
95
96
93
92
99
若成绩为x分，当x≥90时记为A等级，80≤x＜90时记为B等级，70≤x＜80时记为C等级，x＜70时记为D等级，根据表格信息，解答下列问题：
①本次抽样调查获取的样本数据的中位数是；估计全年级本次体育测试成绩在A、B两个等级的人数是；
②经过一个多月的强化训练发现D等级的同学平均成绩提高15分，C等级的同学平均成绩提高10分，B等级的同学平均成绩提高5分，A等级的同学平均成绩没有变化，请估计强化训练后全年级学生的平均成绩提高多少分 ？
23. 某汽车销售公司销售某厂家的某款汽车，该款汽车现在的售价为每辆27万元，每月可售出两辆．市场调查反映：在一定范围内调整价格，每辆降低0.1万元，每月能多卖一辆．已知该款汽车的进价为每辆25万元．另外，月底厂家根据销售量一次性返利给销售公司，销售量在10辆以内（含10辆），每辆返利0.5万元：销售量在10辆以上，超过的部分每辆返利1万元．设该公司当月售出x辆该款汽车．（总利润＝销售利润十返利）(1)、设每辆汽车的销售利润为y万元，求y与x之间的函数关系式；(2)、当x＞10时，该公司当月销售这款汽车所获得的总利润为20.6万元，求x的值．24. 在正边形ABCD中，E是对角线AC上一点（不与点A、C重合），以AD、AE为邻边作平行四边形AEGD ， GE交CD于点M ， 连接CG ．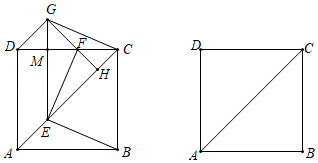
(1)、如图1，当AE＜ AC时，过点E作EF⊥BE交CD于点F ， 连接GF并延长交AC于点H ．①求证：EB＝EF；
②判断GH与AC的位置关系，并证明．
(2)、过点A作AP⊥直线CG于点P ， 连接BP ， 若BP＝10，当点E不与AC中点重合时，求PA与PC的数量关系．25. 已知抛物线y＝﹣ （x+5）（x﹣m）（m＞0）与x轴交于点A、B（点A在点B的左边），与y轴交于点C ．(1)、直接写出点B、C的坐标；（用含m的式子表示）(2)、若抛物线与直线y＝ x交于点E、F ， 且点E、F关于原点对称，求抛物线的解析式；(3)、若点P是线段AB上一点，过点P作x轴的垂线交抛物线于点M ， 交直线AC于点N ， 当线段MN长的最大值为 时，求m的取值范围．