备考2020年中考数学二轮复习拔高训练卷 专题8 圆
试卷更新日期：2020-04-15 类型：二轮复习
一、单选题
-
1. 如图A，B，C是 上的三个点，若 ，则 等于（ ）
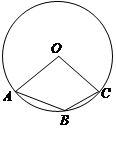A、50° B、80° C、100° D、130°2. 为了测量一个铁球的直径，将该铁球放入工件槽内，测得的有关数据如图所示（单位：cm），则该铁球的直径为（ ）
A、12cm B、10cm C、8cm D、6cm3. 如图，已知在Rt△ABC中，∠BAC=90°，AC=4，BC=5，若把Rt△ABC绕直线AC旋转一周，则所得圆锥的侧面积等于（ ）
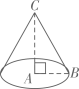A、9π B、12π C、15π D、20π4. 如图，在平面直角坐标系中，已知在矩形ABCD中，AB=2，BC=1，点A从点O开始沿x轴正方向移动，点B在第一象限的角平分线上，求点C到原点O的最大距离（ ）
A、
B、3
C、
D、4
5. 如图，⊙O内切于正方形ABCD，边AD，CD分别与⊙O切于点E，F，点M、N分别在线段DE，DF上，且MN与⊙O相切，若△MBN的面积为8，则⊙O的半径为（ ）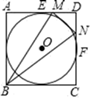
A、 B、2 C、 D、26. 如图，半径为1的⨀O与x轴负半轴，y轴正半轴分别交于点D、E，直线y=kx (k>0)交 ⨀O于A，B，AD，BE的延长线相交于点C，当k的值改变时，下列结论：①∠ACB的度数不变，②CB与CD的比值不变，③CO的长度不变．其中正确的结论的序号是（ ）
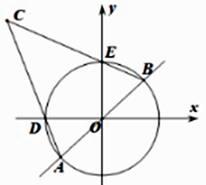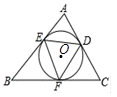
A、1 B、2 C、3 D、07. 如图，MN是半径为2的⊙O的直径，点A在⊙O上，∠AMN＝30°，点B为劣弧AN的中点．点P是直径MN上一动点，则PA＋PB的最小值为（ ）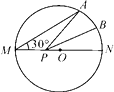
A、4 B、2 C、4 D、28. 如图，⊙O是△ABC的内切圆，切点分别相为点D、E、F，设△ABC的面积、周长分别为S、l，⊙O的半径为r，则下列等式：①∠AED＋∠BFE＋∠CDF＝180°；②S= l r；③2∠EDF＝∠A＋∠C；④2(AD＋CF＋BE)＝l，其中成立的是（ ）
A、①②③④ B、②③④ C、①③④ D、①②③9. 如图，⊙O的半径为2，点A的坐标为(2，2 )，直线AB为⊙O的切线，B为切点，则B点的坐标为（ ）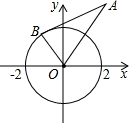
A、(- ) B、(- ，1) C、(- ) D、(-1， )10. 如图， AB是⊙O的直径，且经过弦CD的中点H，已知cos∠CDB＝ ，BD＝5，则OH的长度为（ ）
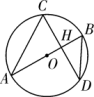A、 B、 C、1 D、11. 如图，在平面直角坐标系中，⊙P与y轴相切，交直线y＝x于A，B两点，已知圆心P的坐标为(2，a)(a＞2)，AB＝2 ，则a的值为（ ）
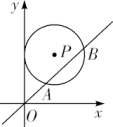A、4 B、2＋ C、 D、12. 如图，在菱形ABCD中，对角线AC，BD交于点O，以OB为直径画⊙M，过点D作⊙M的切线，切点为N，分别交AC，BC于点E、F，已知AE＝5，CE＝3，则DF的长是（ ）
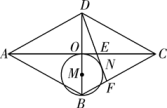A、3 B、4 C、4.8 D、5二、填空题
-
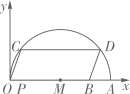
13. 已知△ABC的三边a，b，c满足a+b2+|c-6|+28=4 +10b，则△ABC的外接圆半径=.14. 如图，已知点A的坐标是（10，0），点B的坐标为（8，0），点C、D在以OA为直径的半圆M上，且四边形OCDB是平行四边形，则点C的坐标是。
15. 如图所示，一个宽为2cm的刻度尺在圆形光盘上移动，当刻度尺的一边与光盘相切时，另一边与光盘边缘两个交点处的读数恰好是“2”和“10”（单位：cm），那么该光盘的半径是cm.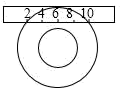
16. 如图，AB是⊙O的直径，点D为⊙O上一点，且∠ABD＝30°，AB＝8，则 的长为 ．
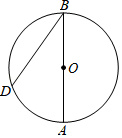17. 如图，AB为半圆O的直径，现将一块等腰直角三角板如图放置，锐角顶点P在半圆上，斜边过点B，一条直角边交该半圆于点Q．若AB＝2，则线段BQ的长为.
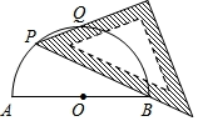18. 如图，这是一个滚珠轴承的示意图，其中内、外圆的半径分别为2和6，如果在内外圆之间放半径为2的滚珠（有阴影的圆表示滚珠），那么在内、外圆之间最多可以放个滚珠.
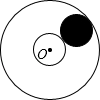19. 如图，在正方形 中， ，分别以 、 为圆心， 长为半径画弧，则图中阴影部分的面积为（结果保留 ）
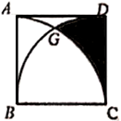20. 如图，在△ABC中，CA=CB，∠ACB=90°，AB=4，点D为AB的中点，以点D为圆心作圆，半圆恰好经过三角形的直角顶点C，以点D为顶点，作90°的∠EDF，与半圆交于点E，F，则图中阴影部分的面积是 ．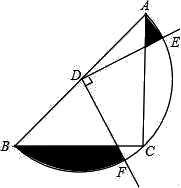
三、综合题
-
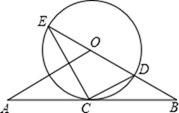
21. 如图，在△ABC中，AB＝AC，O是边AC上的点，以OC为半径的圆分别交边BC、AC于点D、E，过点D作DF⊥AB于点F.
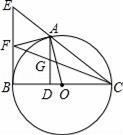
(1)、求证：直线DF是⊙O的切线；(2)、若OC＝1，∠A＝45°，求劣弧DE的长.22. 已知CD为Rt△ABC斜边AB上的高，以CD为直径的圆交BC于E点，交AC于F点，G为BD的中点。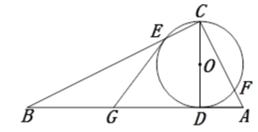
(1)、求证：GE为⊙O的切线；(2)、若tanB=21，GE=5，求AD的长。23. 如图，以Rt△ABC的直角边AB为直径作⊙O交斜边AC于点D，过圆心O作OE∥AC，交BC于点E，连接DE。
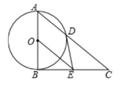(1)、判断DE与⊙O的位置关系并说明理由；(2)、求证：2DE2=CD·OE；(3)、若tanC= ，DE= ，求AD的长。24. 机器人“海宝”在某圆形区域表演“按指令行走”，如图所示，“海宝”从圆心O出发，先沿北偏西67.4°方向行走13米至点A处，再沿正南方向行走14米至点B处，最后沿正东方向行走至点C处，点B、C都在圆O上.（本题参考数据：sin67.4°＝ ，cos67.4°＝ ，tan67.4°＝ ）
(1)、求弦BC的长；(2)、请判断点A和圆的位置关系，试说明理由.
