2020年高考数学二轮复习：15 算法初步、复数、推理与证明

试卷更新日期：2020-04-15 类型：二轮复习

进入出卷网下载

一、单选题

1. 复数 $z$ 满足 $| z | + (z - 1) i = 2$ ，则 $z =$ （）

A、 $1 + \frac{3}{4} i$ B、 $1 - \frac{3}{4} i$ C、 $2 \sqrt{2} +i$ D、 $2 \sqrt{2} - i$

查看试题解析
2. 设 $z = - 3 - 2 i$ ，则在复平面内复数 $\bar{z}$ 对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 已知复数 $z = 1 - i$ ， $\bar{z}$ 为 $z$ 的共轭复数，则 $\frac{1 + z}{\bar{z}} =$ （）

A、 $\frac{3 + i}{2}$ B、 $\frac{1 + i}{2}$ C、 $\frac{1 - 3 i}{2}$ D、 $\frac{1 + 3 i}{2}$

查看试题解析
4. 已知 $a \in R$ ， $i$ 为虚数单位，若复数 $z = \frac{a + i}{1 + i}$ 是纯虚数，则a的值为（）

A、 $- 1$ B、0 C、1 D、2

查看试题解析
5. 执行如图所示的程序框图，若输出s=4，则判断框内应填入的条件是（）

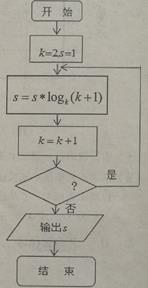A、k≤14 B、k≤15 C、k≤16 D、k<17

查看试题解析
6. 我国古代数学名著《九章算术》里有一个这样的问题：“今有共买金，人出四百，盈三千四百；人出三百，盈一百.问人数、金价几何？”为了解决这个问题，某人设计了如图所示的程序框图，运行该程序框图，则输出的 $x$ ， $y$ 分别为（）

A、30，8900 B、31，9200 C、32，9500 D、33，9800

查看试题解析
7. 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等.如图是源于其思想的一个程序框图，若输入 $a = 4$ ， $b = 1$ ，则输出的 $n$ 等于（）

A、3 B、4 C、5 D、6

查看试题解析
8. 关于甲、乙、丙三人参加高考的结果有下列三个正确的判断：①若甲未被录取，则乙、丙都被录取；②乙与丙中必有一个未被录取；③或者甲未被录取，或者乙被录取.则三人中被录取的是（）

A、甲 B、丙 C、甲与丙 D、甲与乙

查看试题解析
9. 已知函数 $f (2) = \frac{4 x - 2}{4 x^{2} - 4 x + 5} - {(2 x - 1)}^{3} + \frac{1}{2}$ ，则 $\sum_{i = 1}^{2018} f (\frac{k}{2019}) = ($ $)$

A、0 B、1009 C、2018 D、2019

查看试题解析
10. 箱子里有16张扑克牌：红桃 $A$ 、 $Q$ 、4，黑桃 $J$ 、8、7、4、3、2，草花 $K$ 、 $Q$ 、6、5、4，方块 $A$ 、5，老师从这16张牌中挑出一张牌来，并把这张牌的点数告诉了学生甲，把这张牌的花色告诉了学生乙，这时，老师问学生甲和学生乙：你们能从已知的点数或花色中推知这张牌是什么牌吗？于是，老师听到了如下的对话：学生甲：我不知道这张牌；学生乙：我知道你不知道这张牌；学生甲：现在我知道这张牌了；学生乙：我也知道了.则这张牌是（）

A、草花5 B、红桃 $Q$ C、红桃4 D、方块5

查看试题解析
11. 将正偶数排成如图所示的数阵；若第m行第n列位置上的数记为，则该表中的300应记为（   ）
2

4     6      8

10    12    14     16    18

20    22    24     26    28    30    32

……

A、a₁₃⁶ B、a₁₂⁶ C、a₁₃⁷           B.a₁₂⁷

查看试题解析
12. 已知甲、乙、丙三人中，一人是公务员，一人是医生，一人是教师.若丙的年龄比教师的年龄大；甲的年龄和医生的年龄不同；医生的年龄比乙的年龄小，则下列判断正确的是（）

A、甲是公务员，乙是教师，丙是医生 B、甲是教师，乙是公务员，丙是医生 C、甲是教师，乙是医生，丙是公务员 D、甲是医生，乙是教师，丙是公务员

查看试题解析
13. 十七世纪法国数学家费马提出猜想：“当整数 $n > 2$ 时，关于 $x ， y ， z$ 的方程 $x^{n} + y^{n} = z^{n}$ 没有正整数解”.经历三百多年，于二十世纪九十年中期由英国数学家安德鲁 $\cdot$ 怀尔斯证明了费马猜想，使它终成费马大定理，则下面说法正确的是（）

A、存在至少一组正整数组使方程有解 B、关于的方程有正有理数解 C、关于的方程没有正有理数解 D、当整数时，关于的方程没有正实数解

查看试题解析

二、填空题

14. 已知复数 $z = \frac{2}{1 + i} + 2 i$ （ $i$ 是虚数单位），则 $z$ 的共轭复数为．

查看试题解析
15. 若复数 $z = i (3 - 2 i)$ （ $i$ 是虚数单位），则 $z$ 的模为

查看试题解析
16. 天干地支纪年法，源于中国，中国自古便有十天干与十二地支.十天干：甲、乙、丙、丁、戊、己、庚、辛、壬、癸.十二地支：子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支纪年法是按顺序以一个天干和一个地支相配，排列起来，天干在前，地支在后，天干由“甲”起，地支由“子”起，比如第一年为“甲子”，第二年为“乙丑”，第三年为“丙寅”，…，以此类推，排列到“癸酉”后，天干回到“甲”重新开始，即“甲戌”，“乙亥”，之后地支回到“子”重新开始，即“丙子”，…，以此类推，已知2016年为丙申年，那么到改革开放100年时，即2078年为年

查看试题解析
17. 甲、乙、丙三位教师分别在延安、咸阳、宝鸡的三所中学里教不同的学科 $A ， B ， C$ ，已知：①甲不在延安工作，乙不在咸阳工作；②在延安工作的教师不教 $C$ 学科；③在咸阳工作的教师教 $A$ 学科；④乙不教 $B$ 学科.可以判断乙工作地方和教的学科分别是、．

查看试题解析
18. 古代埃及数学中发现有一个独特现象：除 $\frac{2}{3}$ 用一个单独的符号表示外，其它分数都要写成若干个单分数和的形式.例如 $\frac{2}{5} = \frac{1}{3} + \frac{1}{15}$ ，可以这样理解：假定有两个面包，要平均分给5个人，如果每人 $\frac{1}{2}$ ，不够，每人 $\frac{1}{3}$ ，余 $\frac{1}{3}$ ，再将这 $\frac{1}{3}$ 分成5份，每人得 $\frac{1}{15}$ ，这样每人分得 $\frac{1}{3} + \frac{1}{15}$ .形如 $\frac{2}{2 n + 1} (n = 2, 3, 4 \dots)$ 的分数的分解： $\frac{2}{5} = \frac{1}{3} + \frac{1}{15}$ ， $\frac{2}{7} = \frac{1}{4} + \frac{1}{28}$ ， $\frac{2}{9} = \frac{1}{5} + \frac{1}{45}$ ，按此规律， $\frac{2}{2 n + 1} =$ $(n = 2, 3, 4 \dots)$ ．

查看试题解析
19. 已知三个月球探测器 $α, β, γ$ 共发回三张月球照片 $A, B, C$ ，每个探测器仅发回一张照片。
甲说：照片 $A$ 是 $α$ 发回的；

乙说： $β$ 发回的照片不是 $A$ 就是 $B$ ；

丙说：照片 $C$ 不是 $γ$ 发回的。

若甲、乙、丙三人中有且仅有一人说法正确，则照片 $B$ 是探测器发回的。

查看试题解析
20. 意大利著名数学家斐波那契在研究兔子的繁殖问题时，发现有这样的一列数：1，1，2，3，5，8，该数列的特点是：前两个数均为1，从第三个数起，每一个数都等于它前面两个数的和，人们把这样的一列数所组成的数列 ${a_{n}}$ 称为“斐波那契数列”，则 $(a_{1} a_{3} - a_{2}^{2}) + (a_{2} a_{4} - a_{3}^{2}) + (a_{3} a_{5} - a_{4}^{2}) + + (a_{2018} \cdot a_{2020} - a_{2019}^{2}) =$ ．

查看试题解析