2020年高考数学二轮复习：13 概率

试卷更新日期：2020-04-15 类型：二轮复习

进入出卷网下载

一、单选题

1. 如图， $E$ 、 $F$ 、 $G$ 、 $H$ 为正方形 $A B C D$ 各边上的点，图中曲线为圆弧，两圆弧分别以 $B$ 、 $D$ 为圆心， $B O$ 、 $D O$ 为半径（ $O$ 为正方形的中心）.现向该正方形内随机抛掷 $1$ 枚豆子，则该枚豆子落在阴影部分的概率为（）

A、 $\frac{π}{4}$ B、 $\frac{π}{5}$ C、 $\frac{π}{6}$ D、 $\frac{π}{8}$

查看试题解析

2. 中国武汉于2019年10月18日至2019年10月27日成功举办了第七届世界军人运动会.来自109个国家的9300余名运动员同台竞技.经过激烈的角逐，奖牌榜的前3名如下：

国家	金牌	银牌	铜牌	奖牌总数
中国	133	64	42	239
俄罗斯	51	53	57	161
巴西	21	31	36	88

某数学爱好者采用分层抽样的方式，从中国和巴西获得金牌选手中抽取了22名获奖代表.从这22名中随机抽取3人，则这3人中中国选手恰好1人的概率为（）

A、

\frac{22}{57}

B、

\frac{19}{1540}

C、

\frac{57}{1540}

D、

\frac{171}{1540}

查看试题解析

3. 齐王有上等、中等、下等马各一匹，田忌也有上等、中等、下等马各一匹．田忌的上等马优于齐王的中等马，劣于齐王的上等马；田忌的中等马优于齐王的下等马，劣于齐王的中等马，田忌的下等马劣于齐王的下等马．现在从双方的马匹中随机各选一匹进行一场比赛，若有优势的马一定获胜，则齐王的马获胜得概率为（）

A、 $\frac{4}{9}$ B、 $\frac{5}{9}$ C、 $\frac{2}{3}$ D、 $\frac{7}{9}$

查看试题解析
4. 两个实习生每人加工一个零件.加工为一等品的概率分别为 $\frac{5}{6}$ 和 $\frac{3}{4}$ ，两个零件是否加工为一等品相互独立，则这两个零件中恰有一个一等品的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{5}{12}$ D、 $\frac{1}{6}$

查看试题解析
5. 我国数学家陈最润在哥德巴赫猜想的研究中取得了世界瞩目的成就.哥德巴赫猜想简述为“每个大于 $2$ 的偶数可以表示为两个素数的和”(注:如果一个大于 $1$ 的整数除了 $1$ 和自身外无其他正因数，则称这个整数为素数)，如 $40 = 3 + 37$ .在不超过 $40$ 的素数，随机选取 $2$ 个不同的数，这两个数的和等于 $40$ 的概率是（）

A、 $\frac{1}{26}$ B、 $\frac{1}{22}$ C、 $\frac{1}{17}$ D、 $\frac{1}{15}$

查看试题解析
6. 2019年5月22日具有“国家战略”意义的“长三角一体化”会议在芜湖举行；长三角城市群包括：上海市以及江苏省、浙江省、安徽省三省部分城市，简称“三省一市”. 现有4 名高三学生准备高考后到上海市、江苏省、浙江省、安徽省四个地方旅游，假设每名同学均从这四个地方中任意选取一个去旅游，则恰有一个地方未被选中的概率为（）

A、 $\frac{27}{64}$ B、 $\frac{9}{16}$ C、 $\frac{81}{256}$ D、 $\frac{7}{16}$

查看试题解析
7. 割圆术是估算圆周率的科学方法，由三国时期数学家刘徽创立，他用圆内接正多边形面积无限逼近圆面积，从而得出圆周率为 $3.1416$ ，在半径为 $1$ 的圆内任取一点，则该点取自其内接正十二边形的概率为（）

A、 $\frac{1}{π}$ B、 $\frac{3}{π}$ C、 $\frac{\sqrt{3}}{π}$ D、 $\frac{3 \sqrt{3}}{2 π}$

查看试题解析
8. 太极图是以黑白两个鱼形纹组成的图案，它形象化地表达了阴阳轮转、相反相成是万物生成变化根源的哲理，展现了一种相互转化，相对统一的形式美．按照太极图的构图方法，在平面直角坐标系中，圆O被函数 $y = 2 \sin \frac{π}{8} x$ 的图象分割为两个对称的鱼形图案(如图)，其中阴影部分小圆的周长均为 $4 π$ ，现从大圆内随机取一点，则此点取自阴影部分的概率为（）

A、 $\frac{1}{36}$ B、 $\frac{1}{18}$ C、 $\frac{1}{16}$ D、 $\frac{1}{8}$

查看试题解析
9. 若某群体中的成员只用现金支付的概率为0.15，既用现金支付也用非现金支付的概率为0.35，则仅用非现金支付的概率为（）

A、0.2 B、0.4 C、0.5 D、0.8

查看试题解析
10. 《算法统宗》中有一图形称为“方五斜七图”，注曰：方五斜七者此乃言其大略矣，内方五尺外方七尺有奇．实际上，这是一种开平方的近似计算，即用 7 近似表示 $5 \sqrt{2}$ ，当内方的边长为5 时，外方的边长为 $5 \sqrt{2}$ ，略大于7．如图所示，在外方内随机取一点，则此点取自内方的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{5}{7}$ D、 $\frac{25}{49}$

查看试题解析
11. 《西游记》《三国演义》《水浒传》《红楼梦》是我国古典小说四大名著.若在这四大名著中，任取2种进行阅读，则取到《红楼梦》的概率为（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析

二、填空题

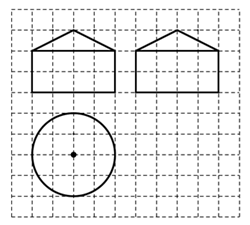
12. 如图，小方格是边长为1的正方形，图中粗线画出的是某几何体的三视图，该几何体是由一个圆锥和一个圆柱组成，若在这个几何体内任取一点，则该点取自圆锥内的概率为．

查看试题解析
13. 近年来，新能源汽车技术不断推陈出新，新产品不断涌现，在汽车市场上影响力不断增大.动力蓄电池技术作为新能源汽车的核心技术，它的不断成熟也是推动新能源汽车发展的主要动力.假定现在市售的某款新能源汽车上，车载动力蓄电池充放电循环次数达到2000次的概率为85%，充放电循环次数达到2500次的概率为35%.若某用户的自用新能源汽车已经经过了2000次充电，那么他的车能够充电2500次的概率为.

查看试题解析
14. 两个男生一个女生并列站成一排，其中两男生相邻的概率为

查看试题解析
15. 某学生选择物理、化学、地理三门学科参加等级考，已知每门学科考 $A^{+}$ 得70分，考 $A$ 得67分，考 $B^{+}$ 得64分，该生每门学科均不低于64分，则其总分至少为207分的概率为

查看试题解析
16. 国产杀毒软件进行比赛，每个软件进行四轮考核，每轮考核中能够准确对病毒进行查杀的进入下一轮考核，否则被淘汰．已知某个软件在四轮考核中能够准确杀毒的概率依次是 $\frac{5}{6}$ ， $\frac{3}{5}$ ， $\frac{3}{4}$ ， $\frac{1}{3}$ ，且各轮考核能否通过互不影响．则该软件至多进入第三轮考核的概率为．

查看试题解析

三、解答题

17. 为了解某中学学生对《中华人民共和国交通安全法》的了解情况，调查部门在该校进行了一次问卷调查（共12道题），从该校学生中随机抽取40人，统计了每人答对的题数，将统计结果分成 $[0 ， 2)$ ， $[2 ， 4)$ ， $[4 ， 6)$ ， $[6 ， 8)$ ， $[8 ， 10)$ ， $[10 ， 12]$ 六组，得到如下频率分布直方图.

(1)、若答对一题得10分，未答对不得分，估计这40人的成绩的平均分（同一组中的数据用该组区间的中点值作代表）；

(2)、若从答对题数在 $[2 ， 6)$ 内的学生中随机抽取2人，求恰有1人答对题数在 $[2 ， 4)$ 内的概率.

查看试题解析
18. 有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.

(1)、将红色卡片和蓝色卡片分别放在两个袋中，然后从两个袋中各取一张卡片，求两张卡片数字之积为偶数的概率

(2)、将五张卡片放在一个袋子中，从中任取两张，求两张卡片颜色不同的概率

查看试题解析

19. 每当《我心永恒》这首感人唯美的歌曲回荡在我们耳边时，便会想起电影《泰坦尼克号》中一暮暮感人画面，让我们明白了什么是人类的“真、善、美”.为了推动我市旅游发展和带动全市经济，更为了向外界传递遂宁人民的“真、善、美”.我市某地将按“泰坦尼克号”原型

1 ： 1

比例重新修建.为了了解该旅游开发在大众中的熟知度，随机从本市

20 \sim 70

岁的人群中抽取了

a

人，得到各年龄段人数的频率分布直方图如图所示，现让他们回答问题“该旅游开发将在我市哪个地方建成？”，统计结果如下表所示：

组号	分组	回答正确的人数	回答正确的人数占本组的频率
第 $1$ 组	$[20 ， 30)$	$10$	$0.5$
第 $2$ 组	$[30 ， 40)$	$x$	$0.9$
第 $3$ 组	$[40 ， 50)$	$54$	$m$
第 $4$ 组	$[50 ， 60)$	$n$	$0.36$
第 $5$ 组	$[60 ， 70)$	$y$	$0.2$

(1)、求出

m (x + y + n)

的值；

(2)、从第

2 ， 3 ， 4

组回答正确的人中用分层抽样的方法抽取

6

人，求第

2 ， 3 ， 4

组每组抽取的人数；

(3)、在（2）中抽取的

6

人中随机抽取

2

人，求所抽取的人中恰好没有年龄在

[30 ， 40)

段的概率.

查看试题解析

20. 为了解某市今年初二年级男生的身体素质状况，从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试．经统计，成绩均在2米到12米之间，把获得的所有数据平均分成 $[2 ， 4) ， [4 ， 6) ， [6 ， 8) ， [8 ， 10) ， [10 ， 12]$ 五组，得到频率分布直方图如图所示．

（Ⅰ）如果有4名学生的成绩在10米到12米之间，求参加“掷实心球”项目测试的人数；

（Ⅱ）若测试数据与成绩之间的关系如下表：

测试数据（单位：米）

$(0 ， 6)$

$[6 ， 8)$

$[8 ， 12)$

成绩

不合格

及格

优秀

根据此次测试成绩的结果，试估计从该市初二年级男生中任意选取一人，“掷实心球”成绩为优秀的概率．

（Ⅲ）在（Ⅱ）的条件下，从该市初二年级男生中任意选取两人，假定两人的成绩是否优秀之间没有影响，求两人中恰有一人“掷实心球”成绩为优秀的概率．

查看试题解析

测试数据（单位：米）	$(0 ， 6)$	$[6 ， 8)$	$[8 ， 12)$
成绩	不合格	及格	优秀