2020年高考数学二轮复习:09 点、直线、平面之间的位置关系
试卷更新日期:2020-04-15 类型:二轮复习
一、单选题
-
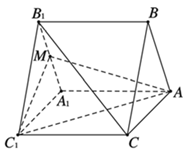
1. 已知直线 平面 ,直线 ,则( )A、 B、 C、 异面 D、 相交而不垂直2. 已知两个不同平面 , 和三条不重合的直线 , , ,则下列命题中正确的是( )A、若 , ,则 B、若 , 在平面 内,且 , ,则 C、若 , , 是两两互相异面的直线,则只存在有限条直线与 , , 都相交 D、若 , 分别经过两异面直线 , ,且 ,则 必与 或 相交3. 、 、 表示空间中三条不同的直线, 、 表示不同的平面,则下列四个命题中正确的是( )A、若 , , ,则 B、若 , , , ,则 C、若 , , , , ,则 D、若 , , , ,则4. 已知正四棱柱 的底面边长为1,高为2, 为 的中点,过 作平面 平行平面 ,若平面 把该正四棱柱分成两个几何体,则体积较小的几何体的体积为( )A、 B、 C、 D、5. 已知三棱锥 的各棱长都相等, 为 中点,则异面直线 与 所成角的余弦值为( )
 A、 B、 C、 D、6. 在棱长为1的正方体 中,异面直线 与 所成的角为( )A、 B、 C、 D、7. 在如图的正方体中,M、N分别为棱BC和棱 的中点,则异面直线AC和MN所成的角为( )
A、 B、 C、 D、6. 在棱长为1的正方体 中,异面直线 与 所成的角为( )A、 B、 C、 D、7. 在如图的正方体中,M、N分别为棱BC和棱 的中点,则异面直线AC和MN所成的角为( ) A、 B、 C、 D、8. 如图,正方体 中, , , , 分别为所在棱的中点,则下列各直线中,不与平面 平行的是( )
A、 B、 C、 D、8. 如图,正方体 中, , , , 分别为所在棱的中点,则下列各直线中,不与平面 平行的是( )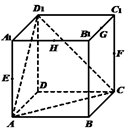 A、直线 B、直线 C、直线 D、直线9. 如图,已知正方体 的棱长为1, 分别是棱 , 上的动点,若 ,则线段 的中点 的轨迹是( )
A、直线 B、直线 C、直线 D、直线9. 如图,已知正方体 的棱长为1, 分别是棱 , 上的动点,若 ,则线段 的中点 的轨迹是( ) A、一条线段 B、一段圆弧 C、一个球面区域 D、两条平行线段10. 如图,在四面体中,若直线 和 相交,则它们的交点一定( )
A、一条线段 B、一段圆弧 C、一个球面区域 D、两条平行线段10. 如图,在四面体中,若直线 和 相交,则它们的交点一定( ) A、在直线 上 B、在直线 上 C、在直线 上 D、都不对11. 在三棱锥 中, , , , ,则三棱锥 外接球的体积的最小值为( )A、 B、 C、 D、12. 如图,在空间四边形 中,点 分别是边 的中点, 分别是边 上的点, ,则( )
A、在直线 上 B、在直线 上 C、在直线 上 D、都不对11. 在三棱锥 中, , , , ,则三棱锥 外接球的体积的最小值为( )A、 B、 C、 D、12. 如图,在空间四边形 中,点 分别是边 的中点, 分别是边 上的点, ,则( ) A、 与 互相平行 B、 与 异面 C、 与 的交点 可能在直线 上,也可能不在直线 上 D、 与 的交点 一定在直线 上
A、 与 互相平行 B、 与 异面 C、 与 的交点 可能在直线 上,也可能不在直线 上 D、 与 的交点 一定在直线 上二、填空题
-
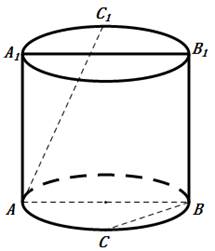
13. 已知三个互不重合的平面 , , ,且直线 , 不重合,由下列条件:① , ;② , ;③ , , ;能推得 的条件是 .14. 如图,已知圆柱的轴截面 是正方形,C是圆柱下底面弧 的中点, 是圆柱上底面弧 的中点,那么异面直线 与 所成角的正切值为.
 15. 已知半径为2的球的球面上有 、 、 、 不同的四点, 是边长为3的等边三角形,且 平面 为球心, 与 在平面 的同一侧),则三棱锥 的体积为.16. 如图,在直三棱柱 中, ,则异面直线 与 所成角的余弦值是 .
15. 已知半径为2的球的球面上有 、 、 、 不同的四点, 是边长为3的等边三角形,且 平面 为球心, 与 在平面 的同一侧),则三棱锥 的体积为.16. 如图,在直三棱柱 中, ,则异面直线 与 所成角的余弦值是 . 17. 《九章算术》中的“邪田”意为直角梯形,上、下底称为畔,高称为正广,非高腰边称为邪。在四棱锥 中,底面 为邪田,两畔 分别为1,3,正广 为 , 平面 ,则邪田 的邪长为;邪所在直线与平面 所成角的大小为.
17. 《九章算术》中的“邪田”意为直角梯形,上、下底称为畔,高称为正广,非高腰边称为邪。在四棱锥 中,底面 为邪田,两畔 分别为1,3,正广 为 , 平面 ,则邪田 的邪长为;邪所在直线与平面 所成角的大小为.三、解答题
-
18. 已知四棱锥 中,四边形 为梯形, ,平面 平面 , 为线段 的中点, .
 (1)、证明: 平面 ;(2)、若 ,求点 到平面 的距离.19. 在四棱锥P﹣ABCD中,底面ABCD为平行四边形,PD⊥平面ABCD,BD=CD,E,F分别为BC,PD的中点.
(1)、证明: 平面 ;(2)、若 ,求点 到平面 的距离.19. 在四棱锥P﹣ABCD中,底面ABCD为平行四边形,PD⊥平面ABCD,BD=CD,E,F分别为BC,PD的中点. (1)、求证:EF∥平面PAB;(2)、求证:平面PBC⊥平面EFD.
(1)、求证:EF∥平面PAB;(2)、求证:平面PBC⊥平面EFD.