2020年高考数学二轮复习：08 空间几何体

试卷更新日期：2020-04-15 类型：二轮复习

进入出卷网下载

一、单选题

1. 某几何体的三视图如图所示，则该几何体的体积为（）

A、 $\frac{π + 4}{12}$ B、 $\frac{π + 1}{3}$ C、 $π + 1$ D、 $\frac{π + 1}{4}$

查看试题解析
2. 已知一几何体的三视图如图所示，它的侧视图与正视图相同，则该几何体的表面积为（）

A、 $16 + 12 π$ B、32+12π C、 $24 + 12 π$ D、32+20π

查看试题解析
3. 直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 的底面是边长为2的正三角形，侧棱长为 $\sqrt{3}$ ， $D$ 为 $B C$ 中点，则三棱锥 $A - B_{1} D C_{1}$ 的体积为（）

A、3 B、 $\frac{3}{2}$ C、1 D、2

查看试题解析
4. 如图所示的三视图表示的几何体的体积为 $\frac{32}{3}$ ，则该几何体的外接球的表面积为（）

A、 $12 π$ B、 $24 π$ C、 $36 π$ D、 $48 π$

查看试题解析
5. 一个由两个圆柱组合而成的密闭容器内装有部分液体，小圆柱底面半径为 $r_{1}$ ，大圆柱底面半径为 $r_{2}$ ，如图1放置容器时，液面以上空余部分的高为 $h_{1}$ ，如图2放置容器时，液面以上空余部分的高为 $h_{2}$ ，则 $\frac{h_{1}}{h_{2}} =$ （）

A、 $\frac{r_{2}}{r_{1}}$ B、 ${(\frac{r_{2}}{r_{1}})}^{2}$ C、 ${(\frac{r_{2}}{r_{1}})}^{3}$ D、 $\sqrt{\frac{r_{2}}{r_{1}}}$

查看试题解析
6. 如图，长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的体积是36，点E在棱 $C C_{1}$ 上，且 $C E = 2 E C_{1}$ ，则三棱锥E-BCD的体积是（）

A、3 B、4 C、6 D、12

查看试题解析
7. 某几何体的正视图和侧视图如图1所示，它的俯视图的直观图是平行四边形 $A^{'} B^{'} C^{'} D^{'}$ ，如图2所示.其中 $A^{'} B^{'} = 2 A^{'} D^{'} = 4$ ，则该几何体的表面积为（）

A、 $16 + 12 π$ B、 $16 + 8 π$ C、 $16 + 10 π$ D、 $8 π$

查看试题解析
8. 某几何体的三视图如图所示，若该几何体的体积为 $\frac{10}{3}$ ，则棱长为a的正方体的外接球的表面积为（）

A、 $12 π$ B、 $14 π$ C、 $4 \sqrt{3} π$ D、 $16 π$

查看试题解析
9. 斗拱是中国古典建筑最富装饰性的构件之一，并为中国所特有．图一图二是斗拱实物图，图三是斗拱构件之一的“斗”的几何体．本图中的斗是由棱台与长方体形凹槽（长方体去掉一个小长方体）组成．若棱台两底面面积分别是400cm² ， 900cm² ，高为9cm ，长方体形凹橹的体积为4300cm³ ，那么这个斗的体积是（）
注：台体体积公式是V $= \frac{1}{3}$ （S' $+ \sqrt{S' S} +$ S）h ．

A、5700cm³ B、8100cm³ C、10000cm³ D、9000cm³

查看试题解析
10. 在四棱锥 $P - A B C D$ 中， $P B = P D = 2$ ， $A B = A D = 1$ ， $P C = \sqrt{3} P A = 3$ ， $∠ B A D = 120 °$ ， $A C$ 平分 $∠ B A D$ ，则四棱锥 $P - A B C D$ 的体积为（）

A、 $\frac{\sqrt{6}}{2}$ B、 $\sqrt{6}$ C、 $\frac{\sqrt{6}}{3}$ D、 $\sqrt{3}$

查看试题解析
11. $《$ 九章算术 $》$ 是我国古代著名数学经典 $.$ 其中对勾股定理的论述比西方早一千多年，其中有这样一个问题：“今有圆材埋在壁中，不知大小 $.$ 以锯锯之，深一寸，锯道长一尺 $.$ 问径几何？”其意为：今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯该材料，锯口深一寸，锯道长一尺 $.$ 问这块圆柱形木料的直径是多少？长为1丈的圆柱形木材部分镶嵌在墙体中，截面图如图所示 $($ 阴影部分为镶嵌在墙体内的部分 $) .$ 已知弦 $A B = 1$ 尺，弓形高 $C D = 1$ 寸，估算该木材镶嵌在墙中的体积约为（）(注：1丈 $= 10$ 尺 $= 100$ 寸， $π \approx 3.14$ ， $sin {22.5}^{\circ} \approx \frac{5}{13}$ )

A、600立方寸 B、610立方寸 C、620立方寸 D、633立方寸

查看试题解析

二、填空题

12. 如图，小方格是边长为1的正方形，图中粗线画出的是某几何体的三视图，正视图中的曲线为四分之一圆弧，则该几何体的表面积是．

查看试题解析
13. 已知某正四棱锥的底面边长和侧棱长均为 $2 c m$ ，则该棱锥的体积为 $c m^{3}$ .

查看试题解析
14. 一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的体积为．

查看试题解析
15. 祖暅是我国南北朝时代的伟大科学家，他在实践的基础上提出了体积计算的原理：“幂势既同，则积不容异”，称为祖暅原理．意思是底面处于同一平面上的两个同高的几何体，若在等高处的截面面积始终相等，则它们的体积相等．利用这个原理求半球O的体积时，需要构造一个几何体，该几何体的三视图如图所示，则该几何体的体积为，表面积为．

查看试题解析
16. 如图，长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的体积是120，E为 $C C_{1}$ 的中点，则三棱锥E-BCD的体积是.

查看试题解析
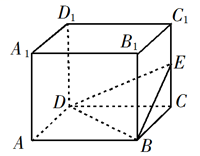17. 学生到工厂劳动实践，利用3D打印技术制作模型，如图，该模型为长方体ABCD-A₁B₁C₁D₁ ，挖去四棱推O一EFGH后所得的几何体，其中O为长方体的中心，E，F，G，H，分别为所在棱的中点，AB=BC=6cm，AA₁=4cm，3D打印所用原料密度为0.9g/cm² ，不考虑打印损耗，制作该模型所需原料的质量为g.

查看试题解析
18. 某三棱锥的三视图如图所示，则该三棱锥体积是，四个面的面积中最大的是.

查看试题解析
19. 在《九章算术》中有称为“羡除”的五面体体积的求法．现有一个类似于“羡除”的有三条棱互相平行的五面体，其三视图如图所示，则该五面体的体积为．

查看试题解析
20. 如图，在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E$ 、 $F$ 分别为棱 $A_{1} D_{1}$ 、 $C_{1} D_{1}$ 的中点， $N$ 是线段 $B C_{1}$ 上的点，且 $B N = \frac{1}{4} B C_{1}$ ，若 $P$ 、 $M$ 分别为线段 $D_{1} B$ 、 $E F$ 上的动点，则 $| P M | + | P N |$ 的最小值为．

查看试题解析