重庆市巴南区2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期:2020-04-14 类型:期中考试
一、单选题
-
1. 25的算术平方根是( )A、5 B、±5 C、± D、2. 下列图形中, 与 不是同位角的是( )A、
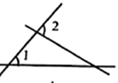 B、
B、 C、
C、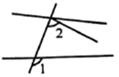 D、
D、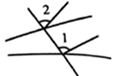 3. 下列说法正确的是( )A、带有根号的数是无理数 B、无限小数是无理数 C、无理数是无限不循环小数 D、无理数是开方开不尽的数4. 如图所示,点E在AB的延长线上,下列条件中不能判断AB//CD的是( )
3. 下列说法正确的是( )A、带有根号的数是无理数 B、无限小数是无理数 C、无理数是无限不循环小数 D、无理数是开方开不尽的数4. 如图所示,点E在AB的延长线上,下列条件中不能判断AB//CD的是( ) A、∠1=∠2 B、∠3=∠4 C、∠C=∠CBE D、∠C+∠ABC=180°5. 将点 先向左平移4个单位长度,再向上平移3个单位长度后得到点 ,则点 的坐标是( )A、 B、 C、 D、6. 若 ,则点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图,小手盖住的点的坐标可能是( )
A、∠1=∠2 B、∠3=∠4 C、∠C=∠CBE D、∠C+∠ABC=180°5. 将点 先向左平移4个单位长度,再向上平移3个单位长度后得到点 ,则点 的坐标是( )A、 B、 C、 D、6. 若 ,则点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图,小手盖住的点的坐标可能是( )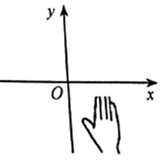 A、 B、 C、 D、8. 若一个正数 的平方根为 和 ,则 ( )A、7 B、16 C、25 D、499. 若 有意义,则 ( )A、 B、 C、0 D、10. 若点 为直线 外一定点,点 为直线 上一定点,且 ,点 到直线 的距离为 ,则 的取值范围为( )A、 B、 或 C、 或 D、 或11. 如图所示,AB∥ED,∠CAB=135°,∠ACD=80°,则∠CDE的度数是( )
A、 B、 C、 D、8. 若一个正数 的平方根为 和 ,则 ( )A、7 B、16 C、25 D、499. 若 有意义,则 ( )A、 B、 C、0 D、10. 若点 为直线 外一定点,点 为直线 上一定点,且 ,点 到直线 的距离为 ,则 的取值范围为( )A、 B、 或 C、 或 D、 或11. 如图所示,AB∥ED,∠CAB=135°,∠ACD=80°,则∠CDE的度数是( )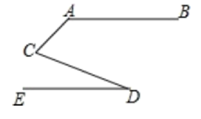 A、 B、 C、 D、12. 如图,在▱ABCD中,BC=7,CD=5,∠D=50°,BE平分∠ABC,则下列结论中不正确的是( )
A、 B、 C、 D、12. 如图,在▱ABCD中,BC=7,CD=5,∠D=50°,BE平分∠ABC,则下列结论中不正确的是( )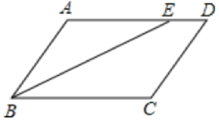 A、∠C=130° B、AE=5 C、∠BED=130° D、ED=2
A、∠C=130° B、AE=5 C、∠BED=130° D、ED=2二、填空题
-
13. 实数27的立方根的相反数是.14. 把命题“对顶角相等”改写成“如果…那么…”的形式:15. 已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B的坐标为.16. 某小区大门的栏杆如图所示, 垂直地面 于 , 平行于地面 ,如果 ,那么 .
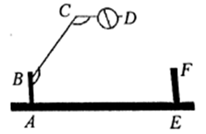 17. 如图,直角三角形DEF是由直角三角形ABC沿BC向右平移3cm得到的,如果AB=6cm,DH=2cm,则图中阴影部分的面积为.
17. 如图,直角三角形DEF是由直角三角形ABC沿BC向右平移3cm得到的,如果AB=6cm,DH=2cm,则图中阴影部分的面积为. 18. 如图,在平面直角坐标系中,动点 在第一象限及 、 轴上运动.第一次它从原点 运到点 ,然后按图中箭头所示方向运动,即 ,每次运动一个单位长度,若第2018次运动到点 ,则式子 的值是.
18. 如图,在平面直角坐标系中,动点 在第一象限及 、 轴上运动.第一次它从原点 运到点 ,然后按图中箭头所示方向运动,即 ,每次运动一个单位长度,若第2018次运动到点 ,则式子 的值是.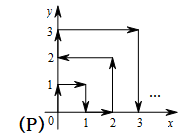
三、解答题
-
19. 计算下列各式:(1)、 ;(2)、 .20. 求下列各式中 的值:(1)、 ;(2)、 .21. 请把下列的证明过程补充完整:
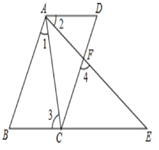
已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4,求证:AD∥BE.
证明:∵AB∥CD(已知)
∴∠4=∠
∵∠3=∠4(已知)
∴∠3=∠(等量代换)
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(等式的性质)
即∠BAF=∠
∴∠3=∠(等量代换)
∴AD∥BE.
22. 已知 的整数部分是a,小数部分是b,求a+ 的值。的整数部分是2,所以 的小数部分是 −2,所以a=2,b= −2,
a+ ,
请根据以上解题提示,解答下题:
已知9+ 与9− 的小数部分分别为a,b,求ab−4a+3b−2的值.
23. 如图,已知点A(−2,4)、B(−4,−1)、C(2,0).将三角形ABC向右平移2个单位长度后,再向下平移3个单位长度,得到三角形A B C ,其中点A 、B 、C 分别是点A.B.C的对应点。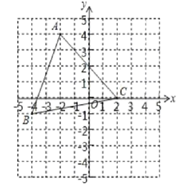 (1)、请在图中画出三角形A B C ,并写出点A 、B 、C 的坐标;(2)、连接AA 、BB ,求四边形AA B B的面积.24. 如图,直线 、 相交于点 , 平分 , .
(1)、请在图中画出三角形A B C ,并写出点A 、B 、C 的坐标;(2)、连接AA 、BB ,求四边形AA B B的面积.24. 如图,直线 、 相交于点 , 平分 , .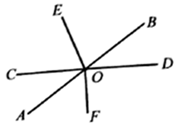 (1)、若∠AOF=50°,求∠BOE的度数;(2)、若∠BOD:∠BOE=1:4,求∠AOF的度数.25. 如图,直线AB和直线BC相交于点B,连接AC,点D.E.H分别在AB、AC、BC上,连接DE、DH,F是DH上一点,已知∠1+∠3=180°,
(1)、若∠AOF=50°,求∠BOE的度数;(2)、若∠BOD:∠BOE=1:4,求∠AOF的度数.25. 如图,直线AB和直线BC相交于点B,连接AC,点D.E.H分别在AB、AC、BC上,连接DE、DH,F是DH上一点,已知∠1+∠3=180°,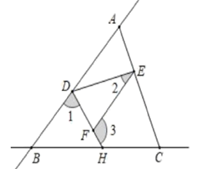 (1)、求证:∠CEF=∠EAD;(2)、若DH平分∠BDE,∠2=α,求∠3的度数.(用α表示).26. (探究活动)
(1)、求证:∠CEF=∠EAD;(2)、若DH平分∠BDE,∠2=α,求∠3的度数.(用α表示).26. (探究活动)如图1:已知直线a与b平行,直线c与直线a、b分别相交于点A.B,直线d与直线a、b分别相交于点C.D,点P在直线c上移动,连接PC、PD.探究∠CPD、∠PCA、∠PDB之间的数量关系.
(探究过程)
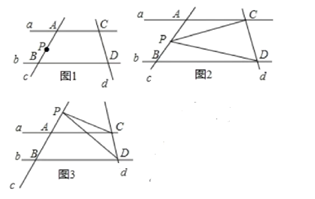 (1)、当点P在点A.B之间移动时,如图2,写出∠CPD、∠PCA、∠PDB之间的关系,并说明理由.(2)、当点P在A.B两点外移动时,如图3,写出∠CPD、∠PCA、∠PDB之间的关系,并说明理由.
(1)、当点P在点A.B之间移动时,如图2,写出∠CPD、∠PCA、∠PDB之间的关系,并说明理由.(2)、当点P在A.B两点外移动时,如图3,写出∠CPD、∠PCA、∠PDB之间的关系,并说明理由.