湖北省宜昌市东部2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期:2020-04-14 类型:期中考试
一、单选题
-
1. 点P(1,﹣5)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下面四个图形中,∠1与∠2是对顶角的是( )A、
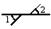 B、
B、 C、
C、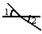 D、
D、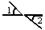 3. 如图,直线 ,直线c是截线,如果 ,那么 等于( )
3. 如图,直线 ,直线c是截线,如果 ,那么 等于( ) A、 B、 C、 D、4. 如图,PO⊥OR,OQ⊥PR,则点O到PR所在直线的距离是线段( )的长.
A、 B、 C、 D、4. 如图,PO⊥OR,OQ⊥PR,则点O到PR所在直线的距离是线段( )的长.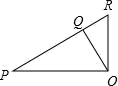 A、OQ B、OR C、OP D、PQ5. 若x轴上的点P到y轴的距离为3,则点P的坐标为( )
A、OQ B、OR C、OP D、PQ5. 若x轴上的点P到y轴的距离为3,则点P的坐标为( )
A、(3,0) B、(3,0)或(–3,0) C、(0,3) D、(0,3)或(0,–3)6. 下列命题中,假命题是( )A、若A(a,b)在x轴上,则B(b,a)在y轴上 B、如果直线a,b,c满足a∥b,b∥c,那么a∥c C、两直线平行,同旁内角互补 D、相等的两个角是对顶角7. 如果甲图形上的点 经平移变换后是 ,则甲图上的点 经这样平移后的对应点的坐标是( )A、 B、 C、 D、8. 如图所示的图案分别是大众、奥迪、奔驰、三菱汽车的车标,其中,可以看作由“基本图案”经过平移得到的是( )A、 B、
B、 C、
C、 D、
D、 9. 计算 的结果是( )A、2 B、±2 C、-2 D、410. 在-1.732, ,π, 3, 2+ ,3.212212221…,3.14这些数中,无理数的个数为( )A、5 B、2 C、3 D、411. 已知下列结论:①在数轴上只能表示无理数 ;②任何一个无理数都能用数轴上的点表示;③实数与数轴上的点一一对应;④有理数有无限个,无理数有有限个.
9. 计算 的结果是( )A、2 B、±2 C、-2 D、410. 在-1.732, ,π, 3, 2+ ,3.212212221…,3.14这些数中,无理数的个数为( )A、5 B、2 C、3 D、411. 已知下列结论:①在数轴上只能表示无理数 ;②任何一个无理数都能用数轴上的点表示;③实数与数轴上的点一一对应;④有理数有无限个,无理数有有限个.其中正确的结论是( ).
A、①② B、②③ C、③④ D、②③④12. 在下列式子中,正确的是( )A、 B、 C、 D、13. 下列说法中,正确的是( )A、不带根号的数不是无理数 B、 的立方根是±2 C、绝对值等于 的实数是 D、每个实数都对应数轴上一个点14. 若 ,则a的取值范围是( )A、 B、 C、 D、15. 能使 有意义的 的范围是( ).A、 且 B、 C、 D、二、解答题
-
16. 计算:(1)、 ;(2)、 ;17. 如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0),C(2,2),将△ABC向左平移1个单位后再向下平移2单位,可得到△A′B′C′.
 (1)、请画出平移后的△A′B′C′的图形;(2)、写出△A′B′C′各个顶点的坐标;(3)、求△ABC的面积.18. 若 ,求 的值.19. 已知 的度数是它补角的3倍, 等于 ,那么 吗?为什么?
(1)、请画出平移后的△A′B′C′的图形;(2)、写出△A′B′C′各个顶点的坐标;(3)、求△ABC的面积.18. 若 ,求 的值.19. 已知 的度数是它补角的3倍, 等于 ,那么 吗?为什么? 20. 如图, , , ,试说明 .
20. 如图, , , ,试说明 . 21. 先阅读下列一段文字,再解答问题
21. 先阅读下列一段文字,再解答问题已知在平面内有两点P1(x1 , y1),P2(x2 , y2),其两点间的距离公式为P1P2= ,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|
(1)、已知点A(2,4),B(﹣3,﹣8),试求A,B两点间的距离;(2)、已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A,B两点间的距离;(3)、已知点A(0,6)B(﹣3,2),C(3,2),判断线段AB,BC,AC中哪两条是相等的?并说明理由.
