湖北省鄂州市梁子湖区2018-2019学年七年级下学期数学期中考试试卷

试卷更新日期：2020-04-14 类型：期中考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点P（ $- \frac{2}{3}$ ，3）所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列图形中，∠1和∠2不是同位角的是（　　）

A、 B、 C、 D、

查看试题解析
3. 在实数－2.5， $\sqrt{13}$ ，3， $\sqrt[3]{27}$ ，3π，0.15， $\frac{1}{3}$ 中，有理数的个数为B，无理数的个数为A，则A－B的值为（）

A、3 B、－3 C、－1 D、1

查看试题解析
4. $2 a - 1$ 和 $a - 5$ 是某个正数的两个平方根，则实数a的值为（）

A、 $\frac{1}{2}$ B、－ $\frac{1}{2}$ C、2 D、－2

查看试题解析
5. 如图，有以下四个条件：①∠B+∠BCD=180°，②∠1=∠2，③∠3=∠4，④∠B=∠5.其中不能判定AB∥CD的条件是（）

A、① B、② C、③ D、④

查看试题解析
6. 若点P关于x轴对称点为P₁（2a+b，3），关于y轴对称点为P₂（9，b+2），则点P坐标为（）

A、（9，3） B、（﹣9，3） C、（9，﹣3） D、（﹣9，﹣3）

查看试题解析
7. 将一张宽度相等的长方形纸条按如图所示的方式折叠一下，如果∠1＝130°，那么∠2的度数是（）

A、105° B、100° C、110° D、115°

查看试题解析
8. 下列四个命题：①如果两个数的绝对值相等，那么这两个数的平方相等；②内错角相等；③在同一平面内，垂直于同一条直线的两条直线平行；④两个无理数的和一定是无理数. 其中真命题的个数是（）

A、4个 B、3个 C、1个 D、2个

查看试题解析
9. 在平面直角坐标系中，把点P（﹣5，2）先向左平移3个单位长度，再向上平移5个单位长度后得到的点的坐标是（　　）

A、（﹣8，6） B、（﹣8，7） C、（﹣2，7） D、（﹣2，﹣3）

查看试题解析
10. 一辆汽车在笔直的公路上行驶，两次拐弯后，仍在原来的方向上平行前进，则两次拐弯的角度可以是（）

A、第一次向右拐40°，第二次向左拐140° B、第一次向左拐40°，第二次向右拐40° C、第一次向左拐40°，第二次向右拐140° D、第一次向右拐40°，第二次向右拐40°

查看试题解析

二、填空题

11. 9的平方根是，使分式 $\frac{1}{x + 1}$ 有意义的x的取值范围是．

查看试题解析
12. 如图，AB∥CD∥EF，若∠ABC＝45°，∠CEF＝155°，则∠BCE的度数为.

查看试题解析
13. 如图所示，已知FD∥BE，那么∠1+∠2﹣∠3＝.

查看试题解析
14. 已知数轴上有A，B两点，且这两点之间的距离为 $5 \sqrt{2}$ ，若点A表示的数为 $2 \sqrt{2}$ ，则点B表示的数为.

查看试题解析
15. 已知∠AOB＝90°，OC为一条射线，OE，OF分别平分∠AOC，∠BOC，那么∠EOF 的度数为.

查看试题解析
16. 如图，在平面直角坐标系中，有若干个横坐标分别为整数的点，其顺序按图中“ $\to$ ”方向排列，如 $(1 ， 0)$ ， $(2 ， 0)$ ， $(2 ， 1)$ ， $(1 ， 1)$ ， $(1 ， 2)$ ， $(2 ， 2) \dots$ 根据这个规律，第2019个点的坐标为.

查看试题解析

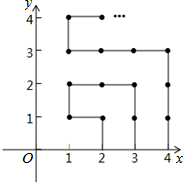
三、解答题

17. 计算：

(1)、 $\sqrt[3]{- \frac{27}{8}}$ ＋ $\sqrt{\frac{4}{9}}$ ＋ $\sqrt{\frac{25}{36}}$ ；

(2)、 $3 (\sqrt{2} - 1) - | \sqrt{2} - 3 | + \sqrt[3]{216}$ .

查看试题解析
18. 解方程：

(1)、 $4 {(x - 3)}^{2} = 64$ ；

(2)、 $3 {(x - 1)}^{3} = 81$ .

查看试题解析
19. 已知：如图，EF∥AD，∠1＝∠2.
求证：∠BAC＝∠DGC.

查看试题解析
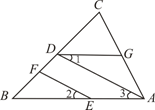20. 已知 $\frac{2 | a^{2} - 16 | + \sqrt{{(a - \frac{1}{2} b)}^{2}}}{\sqrt{4 - a}} = 0$ ，求实数a，b的平方和的倒数.

查看试题解析
21. 如图，已知∠1＝∠BDC，∠2＋∠3＝180°.

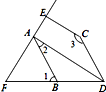(1)、请你判断DA与CE的位置关系，并说明理由；

(2)、若DA平分∠BDC，CE⊥AE于点E，∠1＝70°，试求∠FAB的度数.

查看试题解析
22. 如图，在平面直角坐标系中，△ABO的面积为8，OA＝OB，BC＝12，点P的坐标是（a，6）.

(1)、△ABC三个顶点的坐标分别为A（，），B（，），C（，）；

(2)、是否存在点P，使得 $S_{△ P A B} = S_{△ A B C}$ ？若存在，求出满足条件的所有点P的坐标.

查看试题解析
23. 如图，已知两条射线OM∥CN，动线段AB的两个端点A，B分别在射线OM，CN上，且∠C＝∠OAB＝108°，点E在线段CB上，OB平分∠AOE.

(1)、图中有哪些与∠AOC相等的角？并说明理由；

(2)、若平移AB，那么∠OBC与∠OEC的度数比是否随着AB位置变化而变化？若变化，找出变化规律；若不变，求出这个比值.

查看试题解析
24. 如图，在长方形ABCD中，点A（1，8），B（1，6），C（7，6）.

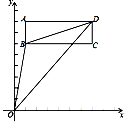(1)、请直接写出点D的坐标；

(2)、连接线段OB，OD，BD，请求出△OBD的面积；

(3)、若长方形ABCD以每秒1个单位长度的速度向下运动，设运动的时间为t秒，是否存在某一时刻，使△OBD的面积与长方形ABCD的面积相等？若存在，请求出t的值；若不存在，请说明理由.

查看试题解析