河南省南阳市邓州市2018-2019学年七年级下学期数学期中考试试卷

试卷更新日期：2020-04-14 类型：期中考试

进入出卷网下载

一、单选题

1. 方程2x﹣1＝﹣5的解是（　　）

A、3 B、﹣3 C、2 D、﹣2

查看试题解析
2. 若x=-2是方程ax-b=1的解，则代数式4a+2b-3的值为（　　）

A、1 B、 $- 3$ C、 $- 1$ D、 $- 5$

查看试题解析
3. 下列四个解方程过程中变形正确的是（　　）

A、由 $- 4 x = 7$ 得 $x = - \frac{4}{7}$ B、由 $\frac{3}{5} x = 4$ 得 $x = \frac{12}{5}$ C、由 $- 2 (x - 1) = - 4$ 得 $x - 1 = 2$ D、由 $2 - 4 x = 7 + x$ 得 $x - 4 x = 7 + 2$

查看试题解析
4. 方程组 ${\begin{array}{l} 2 x + y = ■ \\ x + y = 3 \end{array}$ 的解为 ${\begin{array}{l} x = 2 \\ y = ■ \end{array}$ ，则被遮盖的前后两个数分别为（）

A、1、2 B、1、5 C、5、1 D、2、4

查看试题解析
5. 明铭同学在“求满足不等式-5 $\frac{1}{4}$ ＜x≤-1 $\frac{2}{3}$ 的x的最小整数x₁和最大整数x₂”时，先在如图轴上表示这个不等式的解，然后，很直观的找到了所要求的x₁、x₂的值为（）

A、 $x_{1} = - 5$ ， $x_{2} = - 1$ B、 $x_{1} = - 6$ ， $x_{2} = - 1$ C、 $x_{1} = - 6$ ， $x_{2} = - 2$ D、 $x_{1} = - 5$ ， $x_{2} = - 2$

查看试题解析
6. 若 $a > b$ ，则下列不等式正确的是 $($ 　　 $)$

A、 $a - b < 0$ B、 $a + 8 < b - 8$ C、 $- 5 a < - 5 b$ D、 $\frac{a}{4} < \frac{b}{4}$

查看试题解析
7. 不等式组 ${\begin{array}{l} 4 x - 3 > 1 \\ 6 - 3 x \leq 0 \end{array}$ 的解集在数轴上表示为（　　）

A、 B、 C、 D、

查看试题解析
8. （九章算术》中记载：“今有人共买鸡，人出九，盈十一；人出六，不足十六.问人数、鸡价各几何？”译文：“假设有几个人共同出钱买鸡，如果每人出九钱，那么多了十一钱；如果每人出六钱，那么少了十六钱，问：有几个人共同出钱买鸡？鸡的价钱是多少？”设有x个人共同买鸡，根据题意列一元一次方程，正确的是（　　）

A、 $9 x + l 1 = 6 x - 16$ B、 $9 x - 11 = 6 x + 16$ C、 $\frac{x - 11}{9} = \frac{x + 16}{6}$ D、 $\frac{x + 11}{9} = \frac{x - 16}{6}$

查看试题解析
9. 用白铁皮做罐头盒.每张铁皮可制盒身16个，或制盒底48个，一个盒身与两个盒底配成一套罐头盒.现有15张白铁皮，用制盒身和盒底，可以刚好配多少套？（　　）

A、144套 B、9套 C、6套 D、15套

查看试题解析
10. 不等式-4x-k≤0的负整数解是-1，-2，那么k的取值范围是（　　）

A、 $8 \leq k < 12$ B、 $8 < k \leq 12$ C、 $2 \leq k < 3$ D、 $2 < k \leq 3$

查看试题解析

二、填空题

11. 把方程x+2y-3=0改写成用含x的式子表示y的形式：.

查看试题解析
12. 不等式3x-2≤5x+6的最大负整数解为.

查看试题解析
13. 若不等式（a-3）x＜3-a的解集在数轴上表示如图所示，则a的取值范围是.

查看试题解析
14. 步步高超市在2018年初从科沃斯商城购进一批智能扫地机器人，进价为800元，出售时标价为1200元，后来由于该商品积压，超市准备打折销售，但要保证利润率不低于5%，则至多可打折.

查看试题解析
15. 按下面程序计算，若开始输入x的值为正数，最后输出的结果为656，则满足条件所有x的值是．

查看试题解析

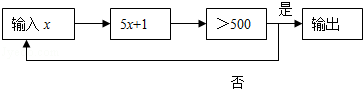
三、解答题

16. 阅读下列解方程组的部分过程，回答下列问题
解方程组 ${\begin{array}{l} x - 2 y = 5 ① \\ 3 x - 2 y = 3 ② \end{array}$

现有两位同学的解法如下：

解法一；由①，得x＝2y+5，③

把③代入②，得3(2y+5)﹣2y＝3.……

解法二：①﹣②，得﹣2x＝2.……

(1)、解法一使用的具体方法是，解法二使用的具体方法是，以上两种方法的共同点是.

(2)、请你任选一种解法，把完整的解题过程写出来

查看试题解析
17. 解方程：

(1)、7-2（3-x)=3(2x -1)

(2)、 $\frac{1 - x}{3} = x + 1 - \frac{3 x - 2}{4}$

查看试题解析
18. 解不等式组 ${\begin{matrix} x - 3 (x - 2) \leq 8 \\ \frac{1}{2} x - 1 < 3 - \frac{3}{2} x \end{matrix}$ ，将解集在数轴上表示出来，并求出此不等式组的所有整数解.

查看试题解析
19. 已知 ${\begin{array}{l} x = - 2 \\ y = - 3 \end{array}$ 和 ${\begin{array}{l} x = 4 \\ y = 1 \end{array}$ 是二元一次方程 $m x - 3 n y = 5$ 的两个解.

(1)、求 $m$ 、 $n$ 的值；

(2)、若 $x < - 2$ ，求 $y$ 的取值范围.

查看试题解析
20. 把正整数1，2，3，4，…排列成如图所示的一个表.

(1)、用一正方形在表中随意框住4个数，把其中最大的数记为x，另三个数用含x的式子表示出来，从大到小依次是，，；

(2)、在（1）的前提下，当被框住的4个数之和等于984时，x位于该表的第几行第几列？

查看试题解析
21. 在推进城乡义务教育均衡发展工作中，我市某区政府通过公开招标的方式为辖区内全部乡镇中学采购了某型号的学生用电脑和教师用笔记本电脑，其中，A乡镇中学更新学生用电脑110台和教师用笔记本电脑32台，共花费30.5万元；B乡镇中学更新学生用电脑55台和教师用笔记本电脑24台，共花费17.65万元.

(1)、求该型号的学生用电脑和教师用笔记本电脑单价分别是多少万元？

(2)、经统计，全部乡镇中学需要购进的教师用笔记本电脑台数比购进的学生用电脑台数的 $\frac{1}{5}$ 少90台，在两种电脑的总费用不超过预算438万元的情况下，至多能购进的学生用电脑和教师用笔记本电脑各多少台？

查看试题解析
22. 为了更好治理河流水质，保护环境，某市治污公司决定购买10台污水处理设备，现有A，B两种型号的设备，其中每台的价格，月处理污水量如表：

A型
B型
价格（万元/台）
a
b
处理污水量（吨/月）
220
180
经调查：购买一台A型设备比购买一台B型设备多3万元，购买2台A型设备比购买3台B型设备少3万元．

(1)、求a，b的值；

(2)、经预算：市治污公司购买污水处理设备的资金不超过100万元，你认为该公司有哪几种购买方案；

(3)、在（2）问的条件下，若每月要求处理的污水量不低于1880吨，为了节约资金，请你为治污公司设计一种最省钱的购买方案．

查看试题解析

23. 根据国家发改委实施“阶梯电价”的有关文件要求，某市结合地方实际，决定从2016年5月1日起对居民生活用电试行新的“阶梯电价”收费，具体收费标准如表：

一户居民一个月用电量的范围	电费价格（单位：元/千瓦时）
不超过150千瓦时的部分	a
超过150千瓦时，但不超过300千瓦时的部分	b
超过300千瓦时的部分	a+0.5

2016年5月份，该市居民甲用电200千瓦时，交费170元；居民乙用电400千瓦时，交费400元.

(1)、求上表中a、b的值：

(2)、试行“阶梯电价”收费以后，该市一户居民月用电多少千瓦时，其当月的平均电价每千瓦时不超过0.85元？

查看试题解析

	A型	B型
价格（万元/台）	a	b
处理污水量（吨/月）	220	180