湖北省宜昌市东部2019届九年级下学期数学期中考试试卷

试卷更新日期：2020-04-14 类型：期中考试

进入出卷网下载

一、单选题

1. 下列实数中的无理数是（）

A、0.7 B、 $\frac{1}{2}$ C、π D、－8

查看试题解析
2. 据统计，2018年3月，三峡大坝共接待旅游人数约4 700 000人次，4 700000这个数用科学记数法表示为（）

A、47×10⁶ B、4.7×10⁵ C、4.7×10⁷ D、4.7×10⁶

查看试题解析
3. 下列图形中，既是轴对称图形又是中心对称图形的是（）.

A、 B、 C、 D、

查看试题解析
4. 有一个正方体，6个面上分别标有1～6这6个整数，投掷这个正方体一次，则出现向上一面的数字是奇数的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
5. 下列算式中，结果等于 $a^{8}$ 的是（）

A、 $a^{4} + a^{4}$ B、 $a^{4} + a^{2} + a^{2}$ C、 $a^{4} \cdot a^{2}$ D、 ${(a^{4})}^{2}$

查看试题解析
6. 若分式 $\frac{x - 3}{x + 3}$ 的值为0，则x的值为 $($ $)$

A、3 B、 $- 3$ C、3或 $- 3$ D、0

查看试题解析
7. 甲、乙、丙、丁四人进行射击测试，每人10次射击的平均成绩恰好都是9.2环，方差分别是 $S_{甲}^{2} = 0.56$ ， $S_{乙}^{2} = 0.45$ ， $S_{丙}^{2} = 0.50$ ， $S_{丁}^{2} = 0.60$ ；则成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 不等式组 ${\begin{matrix} x + 1 > 0 \\ x - 1 < 0 \end{matrix}$ 的解集是（）

A、 $x >$ -1 B、-1＜ $x$ ＜1 C、 $x$ ＞3 D、 $x$ ＜3

查看试题解析
9. 点P（1，-3）在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图像上，则 $k$ 的值是（）

A、 $- \frac{1}{3}$ B、3 C、-2 D、-3

查看试题解析
10. 如图，平行四边形ABCD中，AC，BD为对角线，BC=3，BC边上的高为2，则阴影部分的面积为（）

A、3 B、4 C、6 D、12

查看试题解析
11. 如图，AB是⊙O的弦，半径OC⊥AB于点D，若⊙O的半径为5，AB=8，则CD的长是（）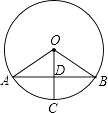

A、2 B、3 C、4 D、5

查看试题解析
12. 如图，矩形 $A B C D$ 的两条对角线相交于点 $O$ ， $∠ A O D = 120^{\circ}$ ， $A B = 2$ ，则矩形的对角线 $A C$ 的长是（）

A、2 B、4 C、2 $\sqrt{3}$ D、4 $\sqrt{3}$

查看试题解析
13. 下列尺规作图，能判断AD是△ABC边上的高是（　　）

A、 B、 C、 D、

查看试题解析
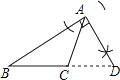14. 在一个不透明的布袋中装有红色.白色玻璃球共40个，除颜色外其他完全相同，小明通过多次摸球试验后发现，其中摸到白色球的频率稳定在85％左右，则口袋中红色球可能有（）.

A、34个 B、30个 C、10个 D、6个

查看试题解析
15. 下图是一组有规律的图案，第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，……，则组成第4个图案的基础图形的个数为（）.

A、11 B、12 C、13 D、14

查看试题解析

二、解答题

16. 先化简，再求值： $(a - 2) (a + 2) - a (a - 2)$ ，其中 $a = - 2$ .

查看试题解析
17. 开学初，小明和小亮去文具店购买学习用品.小明用17元买了1支中性笔和3本笔记本；小亮用29元买了同样的中性笔2支和笔记本5本.求每支中性笔和每本笔记本的价格.

查看试题解析
18. 如图，在边长为1的正方形网格中，

①把△ABC向右平移4个单位长度得到△A´B´C´，在图上画出△A´B´C´，直接写出点A´，B´，C´的坐标；

②将△ABC绕点C顺时针旋转90^o ，得到△A´´B´´C，在图上画出△A´´B´´C，直接写出点A´´，B´´的坐标.

查看试题解析
19. 已知：如图，E、F是四边形ABCD的对角线AC上的两点，AF=CE，DF=BE，DF∥BE.

求证：

(1)、△AFD≌△CEB.

(2)、四边形ABCD是平行四边形.

查看试题解析
20. 某校为了解九年级学生体育测试情况，以901班学生的体育测试成绩为样本，按A.B.C.D四个等级进行统计，并将结果绘制如下两幅统计图，请你结合图中所给信息解答下列问题：（A级：90分及以上；B级：75分～89分；C级：60分～74分；D级：60分以下.注：分数均为整数值）

(1)、请把条形统计图补充完整；

(2)、求样本中D级的学生人数占全班学生人数的百分比；

(3)、求扇形统计图中A级所在的扇形的圆心角度数；

(4)、若该校九年级有400名学生，且75分及以上记为“满分”，请你用此样本估计该校体育测试中获得“满分”的学生人数.

查看试题解析
21. 如图，双曲线 $y = \frac{k}{x} (k > 0)$ 经过矩形OABC的边BC的中点E，交AB于点D.设点B的坐标为（m，n）.

(1)、直接写出点E的坐标，并求出点D的坐标；（用含m，n的代数式表示）

(2)、若梯形ODBC的面积为 $3 \sqrt{5}$ ，求双曲线的函数解析式.

查看试题解析
22. 南.北两个园林场去年共有员工500人，其中南园林场员工数比北园林场员工数的2倍少100人.

(1)、求去年南.北两个园林场的员工数；

(2)、经核算，去年南园林场年产值比北园林场年产值少m%.北园林场人均产值比南园林场人均产值多4m%，且两个园林场人均产值不低于北园林场人均产值的 $\frac{2}{3}$ .求m的值.

查看试题解析
23. 如图，已知，矩形ABCD中，F是对角线BD上一点，以F为圆心，FB为半径作圆与边AD相切于E，边AB与圆F交于另一点G.

(1)、若四边形BGEF是菱形，求证：∠EFD=60^o；

(2)、若AB=15，AD=36，求AE的长；

(3)、若BD与圆F交于另一点H，求证： $\frac{A E}{E D} = \frac{A G}{D H}$ .

查看试题解析
24. 如图，已知：P（-1，0），Q（0，-2）.

(1)、求直线PQ的函数解析式；

(2)、如果M（0， $m$ ）是线段OQ上一动点，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 经过点M和点P，
①求抛物线 $y = a x^{2} + b x + c$ 与 $x$ 轴另一交点N的坐标（用含 $a$ ， $m$ 的代数式表示）；

②若PN= $\frac{1}{2}$ 是，抛物线 $y = a x^{2} + b x + c$ 有最大值 $m$ +1，求此时 $a$ 的值；

③若抛物线 $y = a x^{2} + b x + c$ 与直线PQ始终都有两个公共点，求 $a$ 的取值范围.

查看试题解析