辽宁省鞍山市台安县2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期:2020-04-14 类型:期中考试
一、单选题
-
1. 化简 的结果正确的是( )A、﹣2 B、2 C、±2 D、42. 在 ABCD中,∠A=40°,则∠C=( )A、40° B、50° C、130° D、140°3. 下列计算错误的是( )A、3 +2 =5 B、 ÷2= C、(﹣ )2=3 D、 ﹣ =4. 下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是( )A、3、4、5 B、6、8、10 C、5、12、13 D、5、5、75. 已知平行四边形ABCD,AC、BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为矩形的是( )A、∠BAC=∠DCA B、∠BAC=∠DAC C、∠BAC=∠ABD D、∠BAC=∠ADB6. 如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
 A、5 B、25 C、10 +5 D、357. 已知变量x,y满足下面的关系:
A、5 B、25 C、10 +5 D、357. 已知变量x,y满足下面的关系:x
…
-3
-2
-1
1
2
3
…
y
…
1
1.5
3
-3
-1.5
-1
…
则x,y之间的关系用函数表达式表示为( )
A、y= B、y=- C、y=- D、y=8. 如图所示,矩形ABCD中,AE平分 交BC于E, ,则下面的结论:① 是等边三角形;② ;③ ;④ ,其中正确结论有( )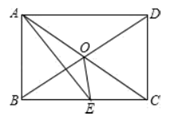 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 计算: =.10. 计算: = .11. 命题“如果两个实数相等,那么它们的平方相等”的逆命题是 ,成立吗 .12. 如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于点D,且AB=4,BD=5,则点D到BC的距离为 .
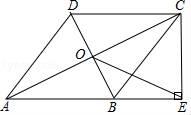
 13. 如图,在▱ABCD中,对角线AC、BD相交于点O,点E是AB的中点,OE=5cm,则AD的长是 cm.
13. 如图,在▱ABCD中,对角线AC、BD相交于点O,点E是AB的中点,OE=5cm,则AD的长是 cm. 14. 小高从家门口骑车去单位上班,先走平路到达点 ,再走上坡路到达点 ,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家门口需要的时间是分钟.
14. 小高从家门口骑车去单位上班,先走平路到达点 ,再走上坡路到达点 ,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家门口需要的时间是分钟.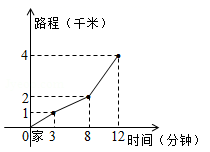 15. 在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是 .16. 如图,正方形ABCD的边长为3,点E在边AB上,且BE=1,若点P在对角线BD上移动,则PA+PE的最小值是 .
15. 在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是 .16. 如图,正方形ABCD的边长为3,点E在边AB上,且BE=1,若点P在对角线BD上移动,则PA+PE的最小值是 .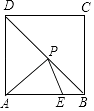
三、解答题
-
17. 计算: ﹣18. 计算:19. 计算:(3 ﹣2 )(3 +2 )﹣( )220. 已知x= ,y= ,求x2﹣3xy+y2的值.21. 如图,在▱ABCD中,AM⊥BD,CN⊥BD,垂足分别为点M,N.求证:四边形AMCN是平行四边形.
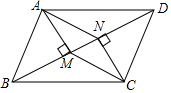 22. 先化简再求值:(a﹣ )÷ ,其中a=1+ ,b=1﹣ .
22. 先化简再求值:(a﹣ )÷ ,其中a=1+ ,b=1﹣ .
23. 如图,在△ABC中,AB=4,AC=3,BC=5,DE是BC的垂直平分线,点D,E分别在BC,AB上,求线段DE的长.