湖北省宜昌市东部2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2020-04-14 类型：期中考试

进入出卷网下载

一、单选题

1. 若代数式 $\sqrt{x - 1}$ 在实数范围内有意义，则 $x$ 的取值范围是 $($ $)$

A、x<1 B、x≤1 C、x>1 D、x≥1

查看试题解析
2. 下列二次根式中，与 $\sqrt{6}$ 是同类二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{18}$ C、 $\sqrt{\frac{2}{3}}$ D、 $\sqrt{30}$

查看试题解析
3. 下列运算正确的是（）

A、 $\sqrt{3}$ × $\sqrt{6}$ =3 $\sqrt{2}$ B、 $\sqrt{12}$ ÷ $\sqrt{3}$ =4 C、3+ $\sqrt{5}$ =3 $\sqrt{5}$ D、 $\sqrt{2}$ + $\sqrt{3}$ = $\sqrt{5}$

查看试题解析
4. 下列三条线段不能构成直角三角形的是（）

A、1、 $\sqrt{3}$ 、2 B、 $\frac{1}{3}$ 、 $\frac{1}{4}$ 、 $\frac{1}{5}$ C、5、12、13 D、9、40、41

查看试题解析
5. 如图，以Rt△ABC为直径分别向外作半圆，若S₁＝10，S₃＝8，则S₂＝（　　）

A、2 B、6 C、 $\sqrt{2}$ D、 $\sqrt{6}$

查看试题解析
6. 在下列性质中，平行四边形不一定具有的是（）

A、对边相等 B、对边平行 C、对角互补 D、内角和为360°

查看试题解析
7. 菱形的周长为8cm，高为1cm，则该菱形两邻角度数比为（）

A、3：1 B、4：1 C、5：1 D、6：1

查看试题解析
8. 在△ABC中，AB＝7，AC＝8，BC＝9，则这个三角形是（　　）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形

查看试题解析
9. 如图．在菱形ABCD中，对角线AC，BD交于点O，下列说法错误的是（）

A、AB∥DC B、AC=BD C、AC⊥BD D、OA=OC

查看试题解析
10. 已知直角三角形中30°角所对的直角边为2cm，则斜边的长为（）

A、2cm B、4cm C、6cm D、8cm

查看试题解析
11. 下列命题中正确的是（）

A、一组对边平行的四边形是平行四边形 B、有一个角是直角的四边形是矩形 C、有一组邻边相等的平行四边形是菱形 D、对角线互相垂直平分的四边形是正方形

查看试题解析
12. 如图，矩形ABCD中，对角线AC，BD交于点O，若∠BOC＝120°，AC＝8，AB的长度是（　　）

A、4 B、4 $\sqrt{2}$ C、4 $\sqrt{3}$ D、8

查看试题解析
13. 如图，数轴上点A对应的数为2，AB⊥OA于A，且AB＝1，以OB为半径画圆，交数轴于点C，则OC的长为（　　）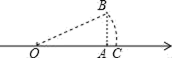

A、3 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、 $\sqrt{5}$

查看试题解析
14. 如图，O是矩形ABCD的对角线AC的中点，M是AD的中点，若AB＝5，AD＝12，则四边形ABOM的周长为（　　）

A、17 B、18 C、19 D、20

查看试题解析
15. 如图，已知△ABC中，AB＝AC，∠BAC＝90°，直角∠EPF的顶点P是BC中点，两边PE、PF分别交AB、AC于点E、F，当∠EPF在△ABC内绕顶点P旋转时（点E不与A、B重合），给出以下四个结论：①AE＝CF；②△EPF是等腰直角三角形；③2S_四边形_AEPF＝S_△_ABC；④BE+CF＝EF.上述结论中始终正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、解答题

16. 计算：

(1)、 $\sqrt{3} （ \sqrt{6}$ ﹣ $\sqrt{3}$ ）+（ $\sqrt{2}$ +1）².

(2)、（ $\sqrt{50}$ ﹣ $\sqrt{8}$ . ）÷ $\sqrt{2}$

查看试题解析
17. 若 $\sqrt{x - 3}$ ﹣ $\sqrt{3 - x}$ ＝（x﹣y）² ，求x﹣y的值.

查看试题解析
18. 求如图的Rt△ABC的面积.

查看试题解析
19. 如图，在△ABC中，AB＝BC，D、E、F分别是BC、AC、AB边上的中点.

(1)、求证：四边形BDEF是菱形；

(2)、若AB＝12cm，求菱形BDEF的周长.

查看试题解析
20. 正方形ABCD中，AB＝4，对角线交于点O，F是BO的中点，连接AF，求AF的长度.

查看试题解析
21. 在△ABC中，∠C＝90°，AC＝6，BC＝8，D、E分别是斜边AB和直角边CB上的点，把△ABC沿着直线DE折叠，顶点B的对应点是B′.

(1)、如图（1），如果点B′和顶点A重合，求CE的长；

(2)、如图（2），如果点B′和落在AC的中点上，求CE的长.

查看试题解析
22. 在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF＝∠CEF＝45°.

(1)、将△ADF绕着点A顺时针旋转90°，得到△ABG（如图①），求证：△AEG≌△AEF；

(2)、若直线EF与AB，AD的延长线分别交于点M，N（如图②），求证：EF²＝ME²+NF².

查看试题解析
23. 如图，在△ABC中，∠BAC＝90°，AB＝AC，D是AC边上一动点，CE⊥BD于E.

(1)、如图（1），若BD平分∠ABC时，
①求∠ECD的度数；

②延长CE交BA的延长线于点F，补全图形，探究BD与EC的数量关系，并证明你的结论；

(2)、如图（2），过点A作AF⊥BE于点F，猜想线段BE，CE，AF之间的数量关系，并证明你的猜想.

查看试题解析
24. 如图，在四边形ABCD中，E、F分别为对角线BD上的两点，且BE＝DF.

(1)、若四边形AECF是平行四边形，求证：四边形ABCD是平行四边形；

(2)、若四边形AECF是菱形，则四边形ABCD是菱形吗？请说明理由？

(3)、若四边形AECF是矩形，则四边形ABCD是矩形吗？不必写出理由.

查看试题解析