湖北省孝感市云梦县2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2020-04-14 类型：期中考试

进入出卷网下载

一、单选题

1. 若二次根式 $\sqrt{x - 3}$ 有意义，则x的取值范围为（）

A、x≥3 B、x≠3 C、x>3 D、x≤3

查看试题解析
2. 已知a≥0，b≥0，下列式子不成立的是（）

A、 ${(\sqrt{a})}^{2} = a$ B、 $\sqrt{a^{2}} = a$ C、 $\sqrt{a} \sqrt{b} = \sqrt{a b}$ D、 $\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}$

查看试题解析
3. 下列四组线段中，可以构成直角三角形的是（）

A、1， $\sqrt{2}$ ，3 B、3，4，5 C、4，5，6 D、6，7，8

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{4} + \sqrt{9} = \sqrt{13}$ B、 $\sqrt{5} - \sqrt{3} = \sqrt{2}$ C、 $\sqrt{3} \cdot \sqrt{2} = \sqrt{6}$ D、 $\sqrt{12} \div \sqrt{6} = 2$

查看试题解析
5. 已知三角形的三边长为a、b、c，如果 ${(a - 5)}^{2} + | b - 12 | + \sqrt{c - 13} = 0$ ，则△ABC是（）

A、以a为斜边的直角三角形 B、以b为斜边的直角三角形 C、以c为斜边的直角三角形 D、不是直角三角形

查看试题解析
6. 一个四边形的三个相邻内角度数依次如下，那么其中是平行四边形的是（）

A、98°，99°，98° B、98°，88°，98° C、98°，82°，82° D、98°，82°，98°

查看试题解析
7. 矩形，菱形，正方形都具有的性质是（）

A、对角线相等 B、对角线互相平分 C、对角线平分组对角 D、四个角都是直角

查看试题解析
8. 设直角三角形的两条直角边长及斜边上的高分别为a，b及h，则下列关系正确的是（）

A、 $\frac{1}{a^{2}} + \frac{1}{b^{2}} = \frac{1}{h^{2}}$ B、 $\frac{1}{a} + \frac{1}{h} = \frac{1}{b}$ C、 $\frac{1}{b^{2}} + \frac{1}{h^{2}} = \frac{1}{a^{2}}$ D、 $\frac{1}{a} + \frac{1}{b} = \frac{1}{h}$

查看试题解析
9. 如图，正方形ABCD的动长为4，G在CD的延长线上，四边形CEFG也是正方形，则△DBF的面积为（）

A、4 B、4 $\sqrt{2}$ C、8 D、8 $\sqrt{2}$

查看试题解析
10. 如好，菱形ABCD，AB=6，∠A=120°，点E，F，G分别为线段BC，CD，BD上的任意一点，则EG+FG的最小值为（）

A、4 B、3 $\sqrt{3}$ C、6 D、4 $\sqrt{3}$

查看试题解析

二、填空题

11. 若代数式 $\frac{\sqrt{x}}{x - 1}$ 有意义，则实数x的取值范围是．

查看试题解析
12. 已知长方形的面积S=4 $\sqrt{3}$ ，一条边长 $a = \sqrt{15}$ ，则相邻的另一边长b=.

查看试题解析
13. 校园内有两棵树，相距8m，一棵树高为13m，另一棵树高7m，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞m.

查看试题解析
14. 如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB=2cm，BC=16cm，则EF=cm.

查看试题解析
15. 下图取材于我国古代数学家赵爽的《勾股圆方图》，由四个全等的直角三角形与中间的小正方形拼成的一个大正方形如果大正方形的面积是13，小正方形的面积是4，直角三角形的较短直角边为a，较长直角边为b，那么 ${(a + b)}^{2}$ 的值为.

查看试题解析
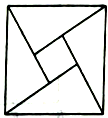16. 如图，将长方形ABCD沿着对角线BD折叠，点C落在C'处，BC′交AD于点E.若AB=4cm，AD=8cm，则△BDE的面积等于.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{18} - \sqrt{\frac{9}{2}}$

(2)、 ${(2 \sqrt{3} + 3 \sqrt{2})}^{2}$

查看试题解析
18. 已知x=2+ $\sqrt{3}$ ，求代数式 $(7 - 4 \sqrt{3}) x^{2} + (2 - \sqrt{3}) x - \sqrt{3}$ 的值.

查看试题解析
19. 如图，在梯形ABCD中，AB∥CD.

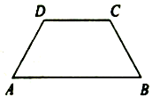(1)、已知∠A=∠B，求证：AD=BC；

(2)、已知AD=BC，求证：∠A=∠B.

查看试题解析
20. 如图，在Rt△ABC中，∠ACB=90°，∠A=30°，BC=3cm，CD⊥AB，在AC上取一点E，使EC=BC，过点E作EF⊥AC交CD的延长线于点F，求EF和AE的长.

查看试题解析
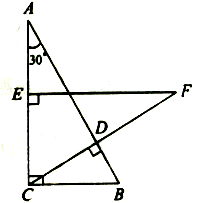21. 如图，在△ABC中，点O是AC边上一动点，过点O作DE，使DE∥BC，DE交∠ACB的角平分线于点D，交∠ACB的外角平分线于点E.

(1)、求证：OD=OE；

(2)、当点O运动到何处时，四边形CDAE是矩形?请证明你的结论.

查看试题解析
22. 如图，在正方形ABCD中，E是BC的中点，F是线段CD上的动点.

(1)、如图1，若CF= $\frac{1}{4}$ CD，求证：ΔAEF是直角三角形；

(2)、如图2，若点F与点D重合，点G在ED上，且AG=AD，求证： $A E^{2} = A D^{2} + E D \cdot E G$ .

查看试题解析
23. 观察下列不等式：
① $\frac{1}{\sqrt{2} + 1} = \frac{\sqrt{2} - 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$

② $\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$

③ $\frac{1}{\sqrt{4} + \sqrt{3}} = \frac{\sqrt{4} - \sqrt{3}}{(\sqrt{4} + \sqrt{3}) (\sqrt{4} - \sqrt{3})} = \sqrt{4} - \sqrt{3}$

…………

回答下列问题：

(1)、利用你观察到的规律，化简 $\frac{1}{3 \sqrt{2} + \sqrt{17}}$ ；

(2)、仿照上列不等式，写出第n个等式：；

(3)、计算： $\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + 2} + ... + \frac{1}{\sqrt{2018} + \sqrt{2019}}$ .

查看试题解析
24. 阅读下列材料：
问题：如图1，在平行四边形ABCD中，E是AD上一点，AE=AB，∠EAB=60°，过点E作直线EF，在EF上取一点G，使得∠EGB=∠EAB，连接AG.

求证：EG=AG+BG.

小明同学的思路是：作∠GAH=∠EAB交GE于点H，构造全等三角形，经过推理解决问题.

参考小明同学的思路，探究并解决下列问题：

(1)、完成上面问题中的证明；

(2)、如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”，原问题中的其它条件不变（如图2），请探究线段EG、AG、BG之间的数量关系，并证明你的结论.

查看试题解析