湖北省武汉市汉阳区2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2020-04-14 类型：期中考试

进入出卷网下载

一、单选题

1. 要使代数式 $\sqrt{x - 2}$ 有意义，则x的取值范围是（）

A、x≠2 B、x≥2 C、x>2 D、x≤2

查看试题解析
2. 下列计算正确的是（　　）

A、 $\sqrt{8} + \sqrt{2} = \sqrt{10}$ B、2 $\sqrt{2} - \sqrt{2} = 2$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{12} \div 2 = \sqrt{6}$

查看试题解析
3. 分别满足下列条件的三角形中，不是直角三角形的是（）

A、三个内角之比为1：2：3 B、三个内角之比为3：4：5 C、三条边长之比为3：4：5 D、三条边长的平方之比为1：2：3

查看试题解析
4. 一个四边形的三个内角的度数依次如下选项，其中是平行四边形的是（）

A、88°，108°，88° B、88°，104°，108° C、88°，92°，92° D、88°，92°，88°

查看试题解析
5. 如图，两把完全一样的直尺叠放在一起，重合的部分构成一个四边形，这个四边形一定是（）

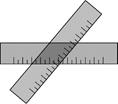A、矩形 B、菱形 C、正方形 D、无法判断

查看试题解析
6. 如图，把一个长方形纸片对折两次，然后沿图中虚线剪下一个角，为了得到一个正方形，剪口与折痕所成的角的大小等于（　　）

A、30° B、45° C、60° D、90°

查看试题解析
7. 如图，在平面直角坐标系xOy中，菱形 $A B C D$ 的顶点 $D$ 在 $x$ 轴上，边 $B C$ 在 $y$ 轴上，若点 $A$ 的坐标为(12，13)，则点 $C$ 的坐标是（）

A、(0，-5) B、(0，-6) C、(0，-7) D、(0，-8)

查看试题解析
8. 如图，在正方形 $A B C D$ 中， $E$ ， $F$ 分别为 $A D$ ， $B C$ 的中点， $P$ 为对角线 $B D$ 上的一个动点，则下列线段的长等于 $A P + E P$ 最小值的是（）

A、 $A B$ B、 $D E$ C、 $B D$ D、 $A F$

查看试题解析
9. 已知ab＜0，则 $\sqrt{a^{2} b}$ 化简后为（）

A、a $\sqrt{b}$ B、﹣a $\sqrt{b}$ C、a $\sqrt{- b}$ D、﹣a $\sqrt{- b}$

查看试题解析
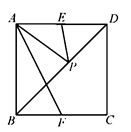10. 如图，已知△ABC中，∠ABC＝90°，AB＝BC，三角形的顶点在相互平行的三条直线l₁ ， l₂ ， l₃上，且l₁ ， l₂之间的距离为2，l₂ ， l₃之间的距离为3，则AC的长是（　　）

A、 $2 \sqrt{17}$ B、 $2 \sqrt{5}$ C、4 $\sqrt{2}$ D、7

查看试题解析

二、填空题

11. 在实数范围内分解因式：x²﹣7＝.

查看试题解析
12. 如图，▱ABCD中，AC、BD相交于点O，若AD=6，AC+BD=16，则△BOC的周长为.

查看试题解析
13. 已知正数a、b，有下列命题：
（ 1 ）如a＝1，b＝1，则 $\sqrt{a b}$ ≤1；（2）若a＝ $\frac{1}{2}$ ，b＝ $\frac{5}{2}$ ，则 $\sqrt{a b} ⩽ \frac{3}{2}$ ；（3）若a＝2，b＝3则 $\sqrt{a b} ⩽ \frac{5}{2}$ ；（4）若a＝1，b＝5，则 $\sqrt{a b}$ ≤3.

根据以上信息，请猜想一个一般性的结论（用含a、b的式子表示）.

查看试题解析
14. 如图，将一张矩形纸片ABCD沿EF折叠后，点C落在AB边上的点G处，点D落在点H处.若∠1＝62°，则图中∠BEG的度数为.

查看试题解析
15. 如右图，一只蚂蚁沿着边长为2的正方体表面从点A出发，经过3个面爬到点B，如果它运动的路径是最短的，则此最短路径的长为.

查看试题解析
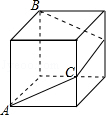16. 如图在△ABC中，∠ACB＝60°，D是AB边的中点，E是边BC上一点，若DE平分△ABC的周长，且DE＝ $\sqrt{3}$ ，则AC的长为.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{2} + \sqrt{8} - \sqrt{18}$

(2)、2 $\sqrt{12} \times \frac{\sqrt{3}}{4} \div 3 \sqrt{2}$

查看试题解析
18. 如图，四边形ABCD为平行四边形，E，F是直线BD上两点，且BE＝DF，连接AF，CE求证：AF＝CE.

查看试题解析
19. 有一块草坪如图所示，已知AB＝6cm，BC＝8cm，CD＝24cm，DA＝26cm，且AB⊥BC，求这块草坪的面积.

查看试题解析
20. 已知：▱ABCD的对角线AC、BD相交于点O，过点D作DP∥OC且DP＝OC，连接CP.得到四边形CODP.

(1)、如图（1），在▱ABCD中，若∠ABC＝90°，判断四边形CODP的形状，并证明；

(2)、如图（2），在▱ABCD中，若AB＝AD，判断四边形CODP的形状，并证明；

(3)、如图（3），在▱ABCD中，若∠ABC＝90°，且AB＝AD，判断四边形CODP的形状，不需证明.

查看试题解析
21. 阅读材料：小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3+2 $\sqrt{2}$ ＝（1+ $\sqrt{2}$ ）² ，善于思考的小明进行了以下探索：设a+ $\sqrt{2}$ b＝（m+ $\sqrt{2}$ n）²（其中a，b，m，n均为正整数），则有a+ $\sqrt{2}$ b＝m²+2n²+2 $\sqrt{2}$ mn，∴a＝m²+2n² ， b＝2mn.这样小明就找到了一种把a+ $\sqrt{2}$ b化为平方式的方法.
请你仿照小明的方法探索并解决下列问题.

(1)、当a、b、m、n均为正整数时，若a+ $\sqrt{3}$ b＝（m+ $\sqrt{3}$ n）² ，用含m、n的式子分别表示a、b，则a＝， b＝；

(2)、求7+4 $\sqrt{3}$ 的算术平方根.

查看试题解析
22. 如图，已知正七边形ABCDEFG，请仅用无刻度的直尺，分别按下列要求画图.

(1)、在图1中，画出一条与AB平行的直线；

(2)、在图2中，画出一个以AB为边的平行四边形；

(3)、在图3中，画出一个以AC为边的菱形.

查看试题解析
23.

(1)、叙述三角形中位线定理，并运用平行四边形的知识证明；

(2)、运用三角形中位线的知识解决如下问题：如图1，在四边形ABCD中，AD∥BC，E、F分别是AB，CD的中点，求证：EF＝ $\frac{1}{2}$ （AD+BC）

(3)、如图2，在四边形ABCD中，AD∥BC，∠B＝90⁰ ， AD＝3，BC＝4，CD＝7，E是AB的中点，直接写出点E到CD的距离.

查看试题解析
24. 对给定的一张矩形纸片ABCD进行如下操作：先沿CE折叠，使点B落在CD边上（如图①），再沿CH折叠，这时发现点E恰好与点D重合（如图②）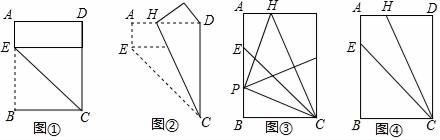

(1)、根据以上操作和发现，求 $\frac{C D}{A D}$ 的值；

(2)、将该矩形纸片展开.
①如图③，折叠该矩形纸片，使点C与点H重合，折痕与AB相交于点P，再将该矩形纸片展开.求证：∠HPC=90°；

②不借助工具，利用图④探索一种新的折叠方法，找出与图③中位置相同的P点，要求只有一条折痕，且点P在折痕上，请简要说明折叠方法.（不需说明理由）

查看试题解析