湖北省随州市2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2020-04-14 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）.

A、 ${(\sqrt{3})}^{2} = 9$ B、 $\sqrt{8} \div \sqrt{2} = 2$ C、 $\sqrt{2} \times \sqrt{3} = 6$ D、 $\sqrt{{(- 2)}^{2}} = - 2$

查看试题解析
2. 下列四组数分别表示三角形的三条边长，其中能构成直角三角形的是(　　)

A、2、3、4 B、2、3、 $\sqrt{7}$ C、 $\sqrt{2}$ 、 $\sqrt{3}$ 、 $\sqrt{5}$ D、1、1、2

查看试题解析
3. 下列命题中，真命题是（）

A、两条对角线相等的四边形是矩形 B、两条对角线互相垂直的四边形是菱形 C、两条对角线互相垂直且相等的四边形是正方形 D、两条对角线互相平分的四边形是平行四边形

查看试题解析
4. 如图，在Rt△ABC中，∠ACB=90∘，以点A为圆心，AC长为半径作圆弧交边AB于点D．若AC=3，BC=4.则BD的长是（）

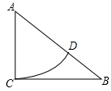A、2 B、3 C、4 D、5

查看试题解析
5. 如图，在▱ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论：（1）2∠DCF=∠BCD，（2）EF=CF；（3）S_△_BEC=2S_△_CEF；（4）∠DFE=3∠AEF，
其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，两张等宽的纸条交叉重叠在一起，重叠的部分为四边形ABCD ，若测得A ， C之间的距离为6cm ，点B ， D之间的距离为8cm ，则线段AB的长为（）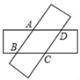

A、5 cm B、4.8 cm C、4.6 cm D、4 cm

查看试题解析
7. 如图：将边长为6的正方形纸片ABCD折叠，使点D落在AB边中点E处，点C落在点Q处，折痕为FH，则线段AF的长是（）

A、2 B、 $\frac{9}{4}$ C、3 D、 $\frac{9}{5}$

查看试题解析
8. 计算 $2 \sqrt{5} \times 3 \sqrt{10}$ =（）

A、 $6 \sqrt{15}$ B、 $6 \sqrt{30}$ C、 $30 \sqrt{2}$ D、 $30 \sqrt{5}$

查看试题解析
9. 实数a在数轴上的位置如图所示，则 $\sqrt{{(a - 3)}^{2}}$ + $\sqrt{{(a - 10)}^{2}}$ 化简后为（）

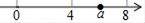A、7 B、﹣7 C、2a﹣15 D、无法确定

查看试题解析
10.
如图，菱形ABCD中，E、F分别是AB、AC的中点，若EF=3，则菱形ABCD的周长是（　　）

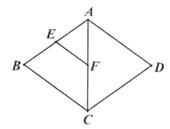A、12 B、16 C、20 D、24

查看试题解析

二、填空题

11. 如图，△ACB和△ECD都是等腰直角三角形，△ACB的锐角顶点A在△ECD的斜边DE上，若AE= $\sqrt{3}$ ，AC= $\sqrt{5}$ ，则DE=.

查看试题解析
12. 把二次根式 $\sqrt{\frac{2}{3}}$ 化成最简二次根式，则 $\sqrt{\frac{2}{3}}$ =.

查看试题解析
13. 如图，在平行四边形ABCD中，AE⊥BC于E，AC＝AD，∠CAE＝56°，则∠D＝.

查看试题解析
14. 由四个全等的直角三角形拼成如图所示的“赵爽弦图”，若直角三角形斜边长为2，最短的边长为1，则图中阴影部分的面积为．

查看试题解析
15. 如图，在Rt△ABC中，∠B=90°，AB=3，BC=4，点D在BC上，以AC为对角线的所有平行四边形ADCE中，DE最小的值是

查看试题解析
16. 如图，已知四边形ABCD中，∠B=90°，AB=3，BC=4，CD=12，AD=13，求四边形ABCD的面积为。

查看试题解析

三、解答题

17. 计算： ${(- 1)}^{0} + | - 4 | - \sqrt{12}$ ；

查看试题解析
18.

(1)、( $\sqrt{50}$ ﹣ $\sqrt{8}$ )+ $\sqrt{2}$

(2)、(2 $\sqrt{5}$ ﹣ $\sqrt{7}$ )(2 $\sqrt{5}$ + $\sqrt{7}$ )﹣( $\sqrt{5}$ ﹣3)².

查看试题解析
19. 如图，在 $▱ A B C D$ 中， $A B = 6$ ， $B C = 8$ ， $A C = 10$ .

(1)、求证：四边形 $A B C D$ 是矩形；

(2)、求 $B D$ 的长.

查看试题解析
20. 如图，▱ABCD中，AB=5，对角线AC=6，BD=8，求▱ABCD的面积.

查看试题解析
21. 如图，在4×4正方形的网格中，线段AB，CD如图位置，每个小正方形的边长都是1.

(1)、求出线段AB、CD的长度；

(2)、在图中画出线段EF，使得EF= $\sqrt{5}$ ，并判断以AB，CD，EF三条线段组成的三角形的形状，请说明理由；

(3)、我们把(2)中三条线段按照点E与点C重合，点F与点B重合，点D与点A重合，这样可以得△ABC，则点C到直线AB的距离为(直接写结果).

查看试题解析
22. 若最简二次根式 $\sqrt[3 x - 10]{2 x + y - 5}$ 和 $\sqrt{x - 3 y + 11}$ 是同类二次根式.

(1)、求x、y的值；

(2)、求 $\sqrt{x^{2} + y^{2}}$ 的值.

查看试题解析
23. 如图所示，等边△ABC的边长为12cm，动点P以每秒2cm的速度从A向B匀速运动，动点Q以每秒1cm的速度从B向C匀速运动，两动点同时出发，当点P到达点B时，所有运动停止.设运动的时间为x秒.

(1)、当运动时间为1秒时，PB＝， BQ＝；

(2)、运动多少秒后，△PBQ恰好为等边三角形？

(3)、运动多少秒后，△PBQ恰好为直角三角形？

查看试题解析
24. 已知：如图，四边形ABCD四条边上的中点分别为E、F、G、H，顺次连接EF、FG、GH、HE，得到四边形EFGH（即四边形ABCD的中点四边形）.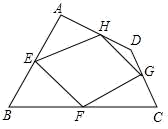

(1)、四边形EFGH的形状是　 ▲ 　，证明你的结论；

(2)、当四边形ABCD的对角线满足条件时，四边形EFGH是矩形；

(3)、你学过的哪种特殊四边形的中点四边形是矩形？（不证明）

查看试题解析
25. 由课本62页练习可知，三角形三条中线交于一点，并且该交点把每条中线分成1：2两部分.如图1：△ABC三边中线AD，BE，CF交于O点，OA=2OD，OB=2OE，OC=2OF.
阅读：我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图2、图3、图4中，AD，BE是△ABC的中线，AD⊥BE垂足为O，像△ABC这样的三角形均为“中垂三角形”.设BC=a，AC=b，AB=c.

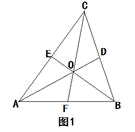(1)、特例探索：如图2，当∠ABE=45°，c=2 $\sqrt{2}$ 时，a= ， b=；

如图3，当∠ABE=30°，c=4时，a= ， b=；

(2)、归纳证明：请你观察（1）中的计算结果，猜想a² ， b² ， c²三者之间的关系，用等式表示出来，并利用图4证明你发现的关系式.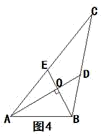

(3)、拓展应用：如图5，▱ABCD中，点E，F，G分别是AD，BC，CD的中点，BE⊥EG，AD=2 $\sqrt{5}$ ，AB=3，求AF的长.

查看试题解析