湖北省黄石市富池片区八校联考2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2020-04-14 类型：期中考试

进入出卷网下载

一、单选题

1. 要使二次根式 $\sqrt{x + 2}$ 有意义，则x的取值范围是（）

A、x＞﹣2 B、x≥﹣2 C、x≠﹣2 D、x≤﹣2

查看试题解析
2. 若 $\sqrt{{(3 - b)}^{2}} = 3 - b$ ，则（）

A、 $b > 3$ B、 $b < 3$ C、 $b \geq 3$ D、 $b \leq 3$

查看试题解析
3. 估算 $\sqrt{7}$ 的值是（）

A、在1和2之间 B、在2和3之间 C、在3和4之间 D、在4和5之间

查看试题解析
4. 已知ab＜0，则 $\sqrt{- a^{2} b}$ 化简后为（）

A、 $- a \sqrt{- b}$ B、 $- a \sqrt{b}$ C、 $a \sqrt{b}$ D、 $a \sqrt{- b}$

查看试题解析
5. 下列命题：①两直线平行，内错角相等；②对角线互相平分的四边形是平行四边形；③全等三角形对应角相等；④平行四边形的两组对边分别相等.其逆命题成立的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，数轴上A表示数﹣2，过数轴上表示1的点B作BC⊥x轴，若BC＝2，以A为圆心，AC为半径作圆弧交数轴于点P，那么数轴上点P所表示的数是（）

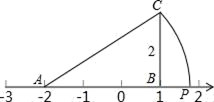A、 $\sqrt{13}$ B、 $\sqrt{13}$ ﹣2 C、 $\sqrt{13}$ ﹣3 D、4﹣ $\sqrt{13}$

查看试题解析
7. 如图，花园住宅小区有一块长方形绿化带，有极少数人为了避开拐角走“捷径”，在草坪内走出了一条“路”.他们仅仅少走了（）步路（假设2步为1米），却踩伤了花草.

A、6步 B、5步 C、4步 D、2步

查看试题解析
8. 如图，在平行四边形ABCD中，BC＝10，AC＝14，BD＝8，则△BOC的周长是（）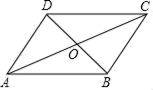

A、21 B、22 C、25 D、32

查看试题解析
9. 如图，把菱形ABCD沿AH折叠，使B点落在BC上的E点处，若∠B＝70°，则∠EDC的大小为（）

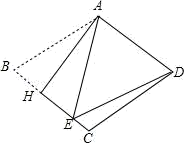A、10° B、15° C、20° D、30°

查看试题解析
10. 已知，在河的两岸有A，B两个村庄，河宽为4千米，A，B两村庄的直线距离AB＝10千米，A，B两村庄到河岸的距离分别为1千米、3千米，计划在河上修建一座桥MN垂直于两岸，M点为靠近A村庄的河岸上一点，则AM+BN的最小值为（）

A、2 $\sqrt{13}$ B、1+3 $\sqrt{5}$ C、3+ $\sqrt{37}$ D、 $\sqrt{85}$

查看试题解析

二、填空题

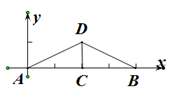
11. 在实数范围内因式分解：x²﹣2= ．

查看试题解析
12. 已知实数a满足|2006﹣a|+ $\sqrt{a - 2007}$ ＝a，则a﹣2006²＝.

查看试题解析
13. 如图，长为8 cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升3 cm到点D，则橡皮筋被拉长了 cm.

查看试题解析
14. 在矩形ABCD中，AB＝8，BC＝10，E是AB上一点，将矩形ABCD沿CE折叠后，点B落在AD边的点F上，则折痕CE的长为.

查看试题解析
15.
将四根木条钉成的长方形木框变形为平行四边形ABCD的形状，并使其面积为长方形面积的一半（木条宽度忽略不计），则这个平行四边形的最小内角为度．

查看试题解析
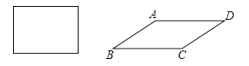16. 如图，正方形ABCD的边长为3cm，E为CD边上一点，∠DAE＝30°，M为AE的中点，过点M作直线分别与AD、BC相交于点P、Q.若PQ＝AE，则AP等于cm.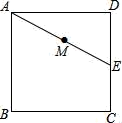

查看试题解析

三、解答题

17. 计算

(1)、2 $\sqrt{3}$ ﹣ $\sqrt{8}$ + $\frac{1}{2} \sqrt{12}$ + $\frac{1}{5} \sqrt{50}$

(2)、 $\sqrt{15}$ ÷（﹣ $\frac{1}{3} \sqrt{6}$ ）× $\frac{3}{5} \sqrt{20}$ .

查看试题解析
18. 已知a，b，c为实数且c＝ $\sqrt{a - 3}$ + $\sqrt{3 - a}$ $- \sqrt{- {(b + 1)}^{2}}$ $+ 2 - \sqrt{5}$ ，求代数式c²﹣ab的值.

查看试题解析
19. 如图，在▱ABCD中，点E，F分别在边BC，AD上，且AF＝CE.
求证：四边形AECF是平行四边形.

查看试题解析
20. 一块试验田的形状如图，已知：∠ABC＝90°，AB＝4m，BC＝3m，AD＝12m，CD＝13m.求这块试验田的面积.

查看试题解析
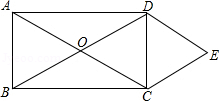
21. 如图，正方形网格的每个小正方形的边长均为1，每个小正方形的顶点叫做格点，图中四条线段的端点均在格点上.

(1)、平移图中的线段，你能使哪三条线段首尾连接构成一个格点三角形，请画出平移后的图形；

(2)、判断并说明三角形的形状.

查看试题解析
22. 如图，矩形ABCD的对角线相交于点O，DE∥AC，CE∥BD.
求证：四边形OCED是菱形.

查看试题解析
23. 如图，有两条公路OM和ON相交成30°角，沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学，当拖拉机沿ON方向行驶时，路两旁50米内会受到噪声影响.已知有两台相距50米的拖拉机正沿ON方向行驶，它们的速度均为5米/秒，问这两台拖拉机沿ON方向行驶时给小学带来噪声影响的时间是多少？

查看试题解析
24.
如图，在Rt△ABC中，∠B=90°，AC=60cm，∠A=60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤15）．过点D作DF⊥BC于点F，连接DE，EF．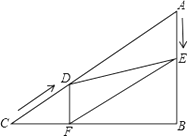

(1)、求证：AE=DF；

(2)、四边形AEFD能够成为菱形吗？如果能，求出相应的t值，如果不能，说明理由；

(3)、当t为何值时，△DEF为直角三角形？请说明理由．

查看试题解析
25. 如图1，在平面直角坐标系xOy中，A（a，0）、B（0，b）、C（﹣a，0），且 $\sqrt{a - 2}$ +b²﹣4b+4＝0

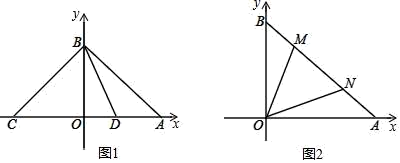(1)、求证：∠ABC＝90°；

(2)、作∠ABO的平分线交x轴于一点D，求D点的坐标；

(3)、如图2所示，A、B两点在x轴、y轴上的位置不变，在线段AB上有两动点M、N，满足∠MON＝45°，下列结论：①BM+AN＝MN；②BM²+AN²＝MN² ，其中有且只有一个结论成立.请你判断哪一个结论成立，并证明成立的结论.

查看试题解析