河南省驻马店市上蔡县2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期:2020-04-14 类型:期中考试
一、单选题
-
1. 下列式子是分式的是( )A、 B、 C、 +y D、2. 如果分式 的值为零,那么 等于( )A、 B、 C、 D、3. 在平面直角坐标系中,点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列y关于x的函数中,是正比例函数的为( )A、y= B、y= C、y= D、y=5. 下列图象中是反比例函数y=﹣ 图象的是( )A、
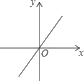 B、
B、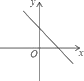 C、
C、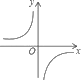 D、
D、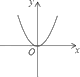 6. 若分式方程 =2+ 有增根,则a的值为( )A、4 B、2 C、1 D、07. 在圆的周长 中,常量与变量分别是( )A、 是常量, 、 是变量 B、 是常量, 、 、 是变量 C、 、 是常量, 是变量 D、 是常量, 、 是变量8. 世界上最小的鸟是生活在古巴的吸蜜蜂鸟,它的质量约为0.056盎司.将0.056用科学记数法表示为( )A、5.6×10﹣1 B、5.6×10﹣2 C、5.6×10﹣3 D、0.56×10﹣19. 如图,平行四边形的对角线 与 相交于点 , ,若 , ,则 的长是( )
6. 若分式方程 =2+ 有增根,则a的值为( )A、4 B、2 C、1 D、07. 在圆的周长 中,常量与变量分别是( )A、 是常量, 、 是变量 B、 是常量, 、 、 是变量 C、 、 是常量, 是变量 D、 是常量, 、 是变量8. 世界上最小的鸟是生活在古巴的吸蜜蜂鸟,它的质量约为0.056盎司.将0.056用科学记数法表示为( )A、5.6×10﹣1 B、5.6×10﹣2 C、5.6×10﹣3 D、0.56×10﹣19. 如图,平行四边形的对角线 与 相交于点 , ,若 , ,则 的长是( )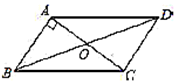 A、 B、 C、 D、10. 如图,在直角坐标系xOy中,点A,B分别在x轴和y轴, . ∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=的图象过点C.当以CD为边的正方形的面积为时,k的值是( )
A、 B、 C、 D、10. 如图,在直角坐标系xOy中,点A,B分别在x轴和y轴, . ∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=的图象过点C.当以CD为边的正方形的面积为时,k的值是( )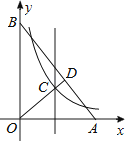 A、2 B、3 C、5 D、7
A、2 B、3 C、5 D、7二、填空题
-
11. 化简: 的结果是.12. 已知:a2﹣3a+1=0,则a+ ﹣2的值为.13. 对于函数 , 的值随 值的增大而.14. 在平行四边形ABCD中,∠A+∠C=200°,则∠A=.15. 如图,反比例函数y= (k≠0)的图象上有一点A,过A作AP⊥x轴于点A,若S△AOP=1,则k=.
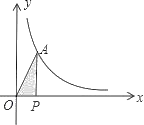 16. 如图,直线 与x轴,y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是.
16. 如图,直线 与x轴,y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是.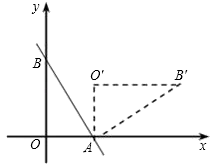
三、解答题
-
17.(1)、20170﹣|﹣2|+( )﹣1;(2)、(2mn2)﹣2n3÷m﹣4.(结果中不出现负整数指数幂)18. 先化简:( )÷ ,再从﹣2,2,﹣1,1中选择一个合适的数代入求值.19. 解方程:20. 我县某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价贵12元,用12000元购进的科普书本数是用9000元购进的文学书本数的 .那么文学书和科普书的单价各是多少元?
21. 如图,在平行四边形 中, 、 的平分线分别交对角线 于点 、 .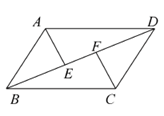
求证: .
22. 某工厂生产一种产品,当生产数量至少为10吨,但不超过50吨时,每吨的成本y(万元/吨)与生产数量x(吨)的函数关系的图象如图所示.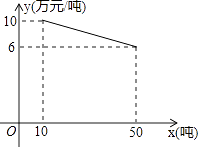 (1)、求y关于x的函数解析式,并写出x的取值范围;
(1)、求y关于x的函数解析式,并写出x的取值范围;
(2)、当生产这种产品每吨的成本为7万元时,求该产品的生产数量.
23. 如图: (1)、利用一次函数的图象解二元一次方程组 .(2)、求图中两条直线与x轴所围成的三角形的面积.24. 已知,在平行四边形 中, 为 上一点,且 ,连接 交 于点 ,过点 作 于 ,交 于点 .
(1)、利用一次函数的图象解二元一次方程组 .(2)、求图中两条直线与x轴所围成的三角形的面积.24. 已知,在平行四边形 中, 为 上一点,且 ,连接 交 于点 ,过点 作 于 ,交 于点 .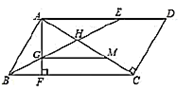 (1)、若 ,求 的度数;(2)、若 ,过点 作 交 于点 ,求证: .25. 已知边长为4的正方形ABCD,顶点A与坐标原点重合,一反比例函数图象过顶点C,动点P以每秒1个单位速度从点A出发沿AB方向运动,动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC﹣CB﹣BA方向顺时针折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.
(1)、若 ,求 的度数;(2)、若 ,过点 作 交 于点 ,求证: .25. 已知边长为4的正方形ABCD,顶点A与坐标原点重合,一反比例函数图象过顶点C,动点P以每秒1个单位速度从点A出发沿AB方向运动,动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC﹣CB﹣BA方向顺时针折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.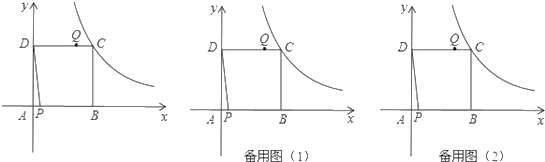 (1)、求出该反比例函数解析式;(2)、连接PD,当以点Q和正方形的某两个顶点组成的三角形和△PAD全等时,求点Q的坐标;(3)、用含t的代数式表示以点Q、P、D为顶点的三角形的面积s,并指出相应t的取值.
(1)、求出该反比例函数解析式;(2)、连接PD,当以点Q和正方形的某两个顶点组成的三角形和△PAD全等时,求点Q的坐标;(3)、用含t的代数式表示以点Q、P、D为顶点的三角形的面积s,并指出相应t的取值.