河南省平顶山市2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2020-04-14 类型：期中考试

进入出卷网下载

一、单选题

1. 下列几个图形是国际通用的交通标志，其中不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 化简 $a \div b \cdot \frac{1}{b}$ 的结果是（　　）

A、 $\frac{a}{b^{2}}$ B、a C、ab² D、ab

查看试题解析
3. 将下列等式从左到右的变形是因式分解的是（　　）

A、4x²+8x﹣1＝4x（x+2）﹣1 B、2ab﹣2ac＝2a（b﹣c） C、（a﹣b）（a+b）＝a²﹣b² D、8a²b⁴＝4a²2b⁴

查看试题解析
4. 若实数a、b满足等式|a﹣3|+ $\sqrt{b - 6}$ ＝0，且a、b恰好是等腰三角形△ABC的边长，则这个等腰三角形的周长是（　　）

A、15 B、9 C、12 D、12或15

查看试题解析
5. 不等式组 ${\begin{array}{l} 3 x - 3 < 0 \\ x + 1 ⩾ 0 \end{array}$ 的解集在数轴上表示正确的是（　　）

A、 B、 C、 D、

查看试题解析
6. 下列命题中正确的是（　　）

A、有两条边相等的两个等腰三角形全等 B、一个锐角和一条边分别相等的两个直角三角形全等 C、一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等 D、两边分别相等的两个直角三角形全等

查看试题解析
7. 某种毛巾原零售价为每条6元，凡一次性购买两条以上，商家推出两种优惠销售办法，第一种：“两条按原价，其余按七折付款”；第二种：“全部按原价的八折付款”.若想在购买相同数量的情况下，要使第一种办法比第二种办法得到的优惠多，最少要购买毛巾（　　）

A、4条 B、5条 C、6条 D、7条

查看试题解析
8. 如图，在△ABC中，AB＝AC，AE平分∠BAC，DE垂直平分AB，连接CE，∠B＝70°.则∠BCE的度数为（　　）

A、55° B、50° C、40° D、35°

查看试题解析
9. 如图，直线 $y = - x + m$ 与 $y = n x + 4 n (n \neq 0)$ 的交点的横坐标为 $- 2$ ，则关于 $x$ 的不等式 $- x + m > n x + 4 n > 0$ 的整数解为（）.

A、 $- 1$ B、 $- 5$ C、 $- 4$ D、 $- 3$

查看试题解析
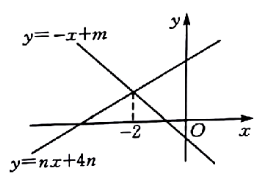10. 如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（）

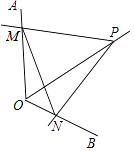A、4 B、3 C、2 D、1

查看试题解析

二、填空题

11. 不等式3x﹣1＞8的解集是.

查看试题解析
12. 已知 $\frac{1}{a} - \frac{1}{b} = \frac{1}{2}$ ，则 $\frac{a b}{a - b}$ 的值是．

查看试题解析
13.
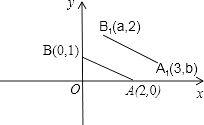
如图，A，B的坐标为（2，0），（0，1）若将线段AB平移至A₁B₁ ，则a+b的值为．

查看试题解析
14. 观察下列各式：2×4＝3²﹣1，3×5＝4²﹣1，4×6＝5²﹣1，…，10×12＝11²﹣1，…，将你猜想到的规律用只含一个字母的式子表示出来：.

查看试题解析
15.
如图，在△ABC中，AB=10，∠B=60°，点D、E分别在AB、BC上，且BD=BE=4，将△BDE沿DE所在直线折叠得到△B′DE（点B′在四边形ADEC内），连接AB′，则AB′的长为

查看试题解析

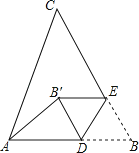
三、解答题

16. 解不等式组，并把解集在数轴上表示出来. ${\begin{array}{l} 3 - x > 0 \\ \frac{5 x + 1}{2} \geq \frac{2 x - 1}{3} \end{array}$

查看试题解析
17. 若a+b＝4，ab＝﹣6，求代数式a³b+2a²b²+ab³的值.

查看试题解析
18. 已知分式 $\frac{x - 1}{2 - 3 x}$ ，回答下列问题.

(1)、若分式无意义，求x的取值范围；

(2)、若分式的值是零，求x的值；

(3)、若分式的值是正数，求x的取值范围.

查看试题解析
19. 如图，图形中每一小格正方形的边长为1，已知△ABC

(1)、AC的长等于．（结果保留根号）

(2)、将△ABC向右平移2个单位得到△A′B′C′，则A点的对应点A′的坐标是；

(3)、画出将△ABC绕点C按顺时针方向旋转90°后得到△A₁B₁C₁ ，并写出A点对应点A₁的坐标？

查看试题解析
20. 如图，已知等腰三角形ABC中，AB=AC，点D、E分别在边AB、AC上，且AD=AE，连接BE、CD，交于点F．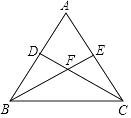

(1)、判断∠ABE与∠ACD的数量关系，并说明理由；

(2)、求证：过点A、F的直线垂直平分线段BC．

查看试题解析
21. 如图，在△ABC中，AE⊥BC于点E，∠B＝22.5°，AB的垂直平分线DN交BC于点D，交AB于点N，DF⊥AC于点F，交AE于点M.求证：

(1)、AE＝DE；

(2)、EM＝EC.

查看试题解析
22. 某公司为奖励在趣味运动会上取得好成绩的员工，计划购买甲、乙两种奖品共20件．其中甲种奖品每件40元，乙种奖品每件30元

(1)、如果购买甲、乙两种奖品共花费了650元，求甲、乙两种奖品各购买了多少件？

(2)、如果购买乙种奖品的件数不超过甲种奖品件数的2倍，总花费不超过680元，求该公司有哪几种不同的购买方案？

查看试题解析
23. 如图1，△ABC的边BC在直线l上，AC⊥BC，且AC＝BC；△EFP的边FP也在直线l上，边EF与边AC重合，且EF＝FP（备注：当EF＝FP，∠EFP＝90°时，∠PEF＝∠FPE＝45°，反之当∠PEF＝∠FPE＝45°时，当EF＝FP）.

(1)、在图1中，请你通过观察、测量、猜想并写出AB与AP所满足的数量关系和位置关系.

(2)、将△EFP沿直线l向左平移到图2的位置时，EP交AC于点Q，连接AP，BQ.猜想并写出BQ与AP所满足的数量关系和位置关系，并证明你的猜想；

(3)、将△EFP沿直线l向左平移到图3的位置时，EP的延长线交AC的延长线于点Q，连接AP、BQ.你认为（2）中所猜想的BQ与AP的结论还成立吗？若成立，给出证明：若不成立，请说明理由.

查看试题解析