河南省南阳市邓州市2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期:2020-04-14 类型:期中考试
一、单选题
-
1. 若分式 的值为0,则x的值为( )A、0 B、1 C、 D、2. 某种细胞的直径是0.000000195米,将0.000000195用科学记数法表示为( )A、1.95× B、1.95× C、0.195× D、1.95×3. 如果把分式 中的a和b的值都变为原来的2倍,则分式的值( )A、不变 B、是原来的 C、是原来的2倍 D、是原来的4倍4. 关于x的分式方程 =1有增根,则m的值为( )A、-6 B、5 C、6 D、45. 如图,已知点A在反比例函数y= 的图象上,点B在反比例函数y= 的图象上,四边形ABCD是长方形,则长方形ABCD的面积是( )
 A、4 B、6 C、8 D、126. 一次函数y=ax+b与反比例函数y= ,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )A、
A、4 B、6 C、8 D、126. 一次函数y=ax+b与反比例函数y= ,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )A、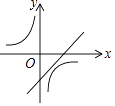 B、
B、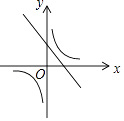 C、
C、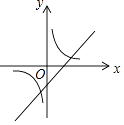 D、
D、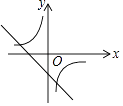 7. ▱ABCD一内角的平分线与边相交并把这条边分成2cm,3cm的两条线段,则▱ABCD的周长是( )A、5cm B、7cm C、14cm或15cm D、14cm或16cm8. 如图,边长为2的正方形 的中心与坐标原点 重合, 轴,将正方形 绕原点 顺时针旋2019次,每次旋转 ,则顶点 的坐标是( )
7. ▱ABCD一内角的平分线与边相交并把这条边分成2cm,3cm的两条线段,则▱ABCD的周长是( )A、5cm B、7cm C、14cm或15cm D、14cm或16cm8. 如图,边长为2的正方形 的中心与坐标原点 重合, 轴,将正方形 绕原点 顺时针旋2019次,每次旋转 ,则顶点 的坐标是( ) A、 B、 C、 D、9. 如图,甲、乙两人以相同路线前往距离单位10km的培训中心参加学习,图中1, 分别表示甲、乙两人前往目的地所走的路程S(千米)随时间(分)变化的函数图象,以下说法:①甲比乙提前12分钟到达;②甲的平均速度为15千米/小时;③甲、乙相遇时,乙走了6千米;④乙出发6分钟后追上甲,其中正确的是( )
A、 B、 C、 D、9. 如图,甲、乙两人以相同路线前往距离单位10km的培训中心参加学习,图中1, 分别表示甲、乙两人前往目的地所走的路程S(千米)随时间(分)变化的函数图象,以下说法:①甲比乙提前12分钟到达;②甲的平均速度为15千米/小时;③甲、乙相遇时,乙走了6千米;④乙出发6分钟后追上甲,其中正确的是( ) A、①② B、③④ C、①③④ D、②③④
A、①② B、③④ C、①③④ D、②③④二、填空题
-
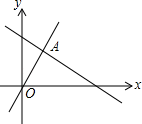
10. 计算 =11. 如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≥ax+4的解集为.
 12. 如图,在▱ABCD中,对角线AC.BD交于点O,点E为BC边上一点,且CE=2BE.若四边形ABEO的面积为3,则▱ABCD的面积为.
12. 如图,在▱ABCD中,对角线AC.BD交于点O,点E为BC边上一点,且CE=2BE.若四边形ABEO的面积为3,则▱ABCD的面积为. 13. 如图,在平面直角坐标系中点 的坐标分别为 ,若直线 与线段 有公共点,则 的取值范围是:.
13. 如图,在平面直角坐标系中点 的坐标分别为 ,若直线 与线段 有公共点,则 的取值范围是:. 14. 如图,在平面直角坐标系中,反比例函数y= (k≠0),经过▱ABCD的顶点B.D,点A的坐标为(0,-1),AB∥x轴,CD经过点(0,2),▱ABCD的面积是18,则点C的坐标是.
14. 如图,在平面直角坐标系中,反比例函数y= (k≠0),经过▱ABCD的顶点B.D,点A的坐标为(0,-1),AB∥x轴,CD经过点(0,2),▱ABCD的面积是18,则点C的坐标是.
三、解答题
-
15.(1)、化简:( +1)÷ ;(2)、解方程: - =1.16. 先化简 ÷( -x+1),然后从- <x< 的范围内选取一个合适的整数作为x的值代入求值.17. 已知一次函数y=2x﹣6,
 (1)、画出该函数的图象.(2)、判断(4,3)是否在此函数的图象上.(3)、观察画出的图象,说一说当x为何值时y<0?18. 如图,反比例函数y= (k为常数,且k≠0)的图象x经过点A(1,4),B(2,m).
(1)、画出该函数的图象.(2)、判断(4,3)是否在此函数的图象上.(3)、观察画出的图象,说一说当x为何值时y<0?18. 如图,反比例函数y= (k为常数,且k≠0)的图象x经过点A(1,4),B(2,m). (1)、求反比例函数的解析式及B点的坐标;(2)、在y轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.19. 某公司开发出一款新的节能产品,该产品在正式投放市场前通过某商场,进行了为期一个月(30天)的试销售,工作人员对销售情况进行了跟踪记录,并将记录情况绘成如图所示的图象.图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系.
(1)、求反比例函数的解析式及B点的坐标;(2)、在y轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.19. 某公司开发出一款新的节能产品,该产品在正式投放市场前通过某商场,进行了为期一个月(30天)的试销售,工作人员对销售情况进行了跟踪记录,并将记录情况绘成如图所示的图象.图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系. (1)、求y与x之间的函数关系式.(2)、哪一天销售量最大?(3)、日销售量不低于320件的天数共有多少天?20. 某商店用2500元采购A型商品的件数是用750元采购B种商品件数数量的2倍,已知一件A型商品的进价比一件B型商品的进价多10元.(1)、求一件A,B型商品的进价分别为多少元?(2)、若商店购进A,B型商品共150件,已知A型商品的售价为30元/件,B型商品的售价为25元/件,且全部售出,设购进A型商品m件,求这批商品的利润W(元)与m之间的函数关系式;(3)、在(2)的条件下,若A型商品的件数不少于B型商品的4倍,请你设计获利最大的进货方案,并求最大利润.21. 如图①▱ABCD的对角线AC和BD相交于点O,EF过点O且与边AB,CD分别相交于点E和点F.
(1)、求y与x之间的函数关系式.(2)、哪一天销售量最大?(3)、日销售量不低于320件的天数共有多少天?20. 某商店用2500元采购A型商品的件数是用750元采购B种商品件数数量的2倍,已知一件A型商品的进价比一件B型商品的进价多10元.(1)、求一件A,B型商品的进价分别为多少元?(2)、若商店购进A,B型商品共150件,已知A型商品的售价为30元/件,B型商品的售价为25元/件,且全部售出,设购进A型商品m件,求这批商品的利润W(元)与m之间的函数关系式;(3)、在(2)的条件下,若A型商品的件数不少于B型商品的4倍,请你设计获利最大的进货方案,并求最大利润.21. 如图①▱ABCD的对角线AC和BD相交于点O,EF过点O且与边AB,CD分别相交于点E和点F. (1)、求证:OE=OF(2)、如图②,已知AD=1,BD=2,AC=2 ,∠DOF=∠α,
(1)、求证:OE=OF(2)、如图②,已知AD=1,BD=2,AC=2 ,∠DOF=∠α,①当∠α为多少度时,EF⊥AC?
②连结AF,求△ADF的周长.
22. 如图,在平面直角坐标系中,一次函数y1=ax+b的图象与x轴,y轴交于A,B;与直线y2=kx交于P(2,1),且PO=PA. (1)、求点A的坐标和k的值;(2)、求a,b的值;(3)、点D为直线y1=ax+b上一动点,其横坐标为m,(m<2),DF⊥x轴于点F,交y2=kx于点E,且DF=3EF,求点D的坐标.
(1)、求点A的坐标和k的值;(2)、求a,b的值;(3)、点D为直线y1=ax+b上一动点,其横坐标为m,(m<2),DF⊥x轴于点F,交y2=kx于点E,且DF=3EF,求点D的坐标.