河南省漯河市郾城区2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2020-04-14 类型：期中考试

进入出卷网下载

一、单选题

1. 如果二次根式 $\sqrt{3 - x}$ 有意义，那么x的取值范围是（　　）

A、x≥0 B、x≥3 C、x≤3 D、x≠3

查看试题解析
2. 下列二次根式中最简二次根式是（　　）

A、 $\sqrt{12 a}$ B、 $\sqrt{1 \frac{1}{3}}$ C、 $\sqrt{2}$ D、 $\sqrt{3 m^{2} n^{3}}$

查看试题解析
3. 在△ABC中，AB=8，BC=15，AC=17，则下列结论正确的是（）

A、△ABC是直角三角形，且∠A=90⁰ B、△ABC是直角三角形，且∠B=90⁰ C、△ABC是直角三角形，且∠C=90⁰ D、△ABC不是直角三角形

查看试题解析
4. 下列计算正确的是（）

A、 $2 \sqrt{3} + 3 \sqrt{2} = 5$ B、 $\sqrt{8} \div \sqrt{2} = 2$ C、 $5 \sqrt{3} \times 5 \sqrt{2} = 5 \sqrt{6}$ D、 $\sqrt{4 \frac{1}{2}} = 2 \sqrt{\frac{1}{2}}$

查看试题解析
5. 矩形具有而平行四边形不具有的性质是（）

A、对角线相等 B、两组对边分别平行 C、对角线互相平分 D、两组对角分别相等

查看试题解析
6. 如图，要测定被池塘隔开的A，B两点的距离.可以在AB外选一点C，连接AC，BC，并分别找出它们的中点D，E，连接DE.现测得AC＝30m，BC＝40m，DE＝24m，则AB＝（　　）

A、50m B、48m C、45m D、35m

查看试题解析
7. 如图，四边形ABCD是菱形，A（3，0），B（0，4），则点C的坐标为（）

A、（－5，4）. B、（－5，5）. C、（－4，4）. D、（－4，3）

查看试题解析
8. 如图，平行四边形ABCD中，E，F分别为AD，BC边上的一点，增加下列条件，不一定能得出BE∥DF的是（　　）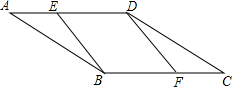

A、AE＝CF B、BE＝DF C、∠EBF＝∠FDE D、∠BED＝∠BFD

查看试题解析
9. 如图，平行四边形 ABCD 中， E为 BC 边上一点，以 AE 为边作正方形AEFG，若 $∠ B A E = 40 °$ ， $∠ C E F = 15 °$ ，则 $∠ D$ 的度数是（）

A、 $65 °$ B、 $55 °$ C、 $70 °$ D、 $75 °$

查看试题解析
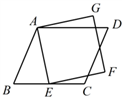10. 已知菱形的周长为4 $\sqrt{5}$ ，两条对角线的和为6，则菱形的面积为（）

A、2 B、 $\sqrt{5}$ C、3 D、4

查看试题解析

二、填空题

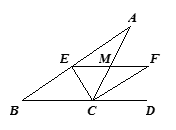
11. 已知x＝ $\sqrt{2}$ ﹣1，则x²+2x+2018＝.

查看试题解析
12. 如图，在△ABC中，CE平分∠ACB，CF平分外角∠ACD，且EF∥BC交AC 于M，若CM=5，则 $C E^{2} + C F^{2} =$ 。

查看试题解析
13. 如图，矩形ABCD的对角线AC、BD相交于点O，DE∥AC，CE∥BD，若BD＝5，则四边形DOCE的周长为·

查看试题解析
14. 如图，已知菱形ABCD的边长为2，∠CDA＝120°，则对角线AC的长为.

查看试题解析
15. 如图，在平面直角坐标系中，四边形OABC是边长为2的正方形，顶点A、C分别在x轴、y轴的正半轴上，点Q在对角线OB上，若OQ=OC，则点Q的坐标为.

查看试题解析

三、解答题

16. 计算：

(1)、 $\sqrt{18} - 4 \sqrt{\frac{1}{2}} + \sqrt{2}$

(2)、 ${(\sqrt{3} + \sqrt{2})}^{2} - (\sqrt{5} + 2) (\sqrt{5} - 2)$

查看试题解析
17. 在计算 $\sqrt{6}$ ×2 $\sqrt{3}$ - $\sqrt{24}$ ÷ $\sqrt{3}$ 的值时，小亮的解题过程如下：
解：原式=2 $\sqrt{6 \times 3}$ - $\sqrt{\frac{24}{3}}$ ……①

=2 $\sqrt{18}$ - $\sqrt{8}$ ……②

=（2-1） $\sqrt{18 - 8}$ ……③

= $\sqrt{10}$ ……④.

(1)、老师认为小亮的解法有错，请你指出：小亮是从第步开始出错的；

(2)、请你给出正确的解题过程.

查看试题解析
18. 如图，学校要把宣传标语掛到教学楼的顶部D处.已知楼顶D处离地面的距离DA为8m，云梯的长度为9m，为保证安全，梯子的底部和墙基的距离AB至少为3m，云梯的顶部能到达D处吗？为什么？

查看试题解析
19. 如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点.

(1)、在图1中以格点为顶点画一个面积为5的正方形；

(2)、在图2中以格点为顶点画一个三角形，使三角形三边长分别为2、 $\sqrt{5}$ 、 $\sqrt{13}$ ；

(3)、如图3，A、B、C是小正方形的顶点，求∠ABC.

查看试题解析
20. 观察下列各式：
$\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} = 1 + \frac{1}{1} - \frac{1}{2} = 1 \frac{1}{2}$ ； $\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = 1 + \frac{1}{2} - \frac{1}{3} = 1 \frac{1}{6}$ ； $\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = 1 + \frac{1}{3} - \frac{1}{4} = 1 \frac{1}{12}$ ；

…

请你根据以上三个等式提供的信息解答下列问题

(1)、猜想： $\sqrt{1 + \frac{1}{7^{2}} + \frac{1}{8^{2}}}$ ＝＝；

(2)、归纳：根据你的观察，猜想，请写出一个用n（n为正整数）表示的等式：；

(3)、应用：计算 $\sqrt{\frac{82}{81} + \frac{1}{100}}$ .

查看试题解析
21. 如图，在△ABC中，D是BC边的中点，分别过B、C做射线AD的垂线，垂足分别为E、F，连接BF、CE.

(1)、求证：四边形BECF是平行四边形；

(2)、我们知道S_△_ABD＝S_△_ACD ，若AF＝FD，在不添加辅助线的条件下，直接写出与△ABD、△ACD面积相等的所有三角形.

查看试题解析
22. 如图，在平行四边形ABCD中，AB＝6，BC＝10，AC⊥AB，点E、F分别是BC，AD上的点，且BE＝DF.

(1)、求证：四边形AECF是平行四边形；

(2)、若四边形AECF是菱形时，请求出AE的长度；

(3)、若四边形AECF是矩形时，请直接写出BE的长度.

查看试题解析
23. 如图1，P为正方形ABCD的边BC上一动点（P与B、C不重合），连接AP，过点B作BQ⊥AP交CD于点Q，将△BQC沿BQ所在的直线对折得到△BQC'，延长QC′交BA的延长线于点M.

(1)、试探究AP与BQ的数量关系，并证明你的结论；

(2)、求证：MQ＝MB；

(3)、若AB＝3，BP＝2PC，求QM的长.

查看试题解析