2018-2019沪科版七年级中期试卷

试卷更新日期：2020-04-13 类型：期中考试

进入出卷网下载

一、选择题

1. 习近平总书记提出了未来五年“精准扶贫”的战略构想，意味着每年要减贫约11700000人，将数据11700000用科学记数法表示为（）

A、1.17×10⁷ B、11.7×10⁶ C、0.117×10⁷ D、1.17×10⁸

查看试题解析
2. ﹣ $\frac{1}{2017}$ 的相反数是（）

A、 $\frac{1}{2017}$ B、﹣ $\frac{1}{2017}$ C、2017 D、﹣2017

查看试题解析
3. 下列各式，去括号正确的是（）

A、a+（b﹣c）+d=a﹣b+c﹣d B、a﹣（b﹣c+d）=a﹣b﹣c+d C、a﹣（b﹣c+d）=a﹣b+c﹣d D、a﹣（b﹣c+d）=a﹣b+c+d

查看试题解析
4. 下列说法正确的是（）

A、有理数是指整数、分数、零、正有理数、负有理数这五类 B、一个有理数不是正数就是负数 C、一个有理数不是整数就是分数 D、以上说法都符合题意

查看试题解析
5. 在一列数：a₁ ， a₂ ， a₃ ， …，a_n中，a₁=3，a₂=7，从第三个数开始，每一个数都等于它前两个数之积的个位数字，则这一列数中的第2017个数是（）

A、1 B、3 C、7 D、9

查看试题解析
6. 计算（﹣16）÷8的结果等于（）

A、 $\frac{1}{2}$ B、﹣2 C、3 D、﹣1

查看试题解析
7. 已知a，b在数轴上的位置如图所示，则a﹣b的结果的符号为（）

A、正 B、负 C、0 D、无法确定

查看试题解析
8.
如图是一个长方形的铝合金窗框，其长为a（m），高为b（m），装有同样大的塑钢玻璃，当第②块向右拉到与第③块重叠 $\frac{1}{2}$ ，再把第①块向右拉到与第②块重叠 $\frac{1}{3}$ 时，用含a与b的式子表示这时窗子的通风面积是（　　）m² ．

A、 $\frac{1}{18} a b$ B、 $\frac{5}{18} a b$ C、 $\frac{13}{18} a b$ D、 $\frac{17}{18} a b$

查看试题解析
9. 如图， $\frac{2}{5}$ 的倒数在数轴上表示的点位于下列两个点之间（）

A、点E和点F B、点F和点G C、点G和点H D、点H和点I

查看试题解析
10. a、b、c、m都是有理数，且a＋2b＋3c＝m ， a＋b＋2c＝m ，那么b与c的关系是（　　）

A、互为相反数 B、互为倒数 C、相等 D、无法确定

查看试题解析
11. 下列运算中，结果为负值的是（）

A、1×（﹣2）÷（﹣3） B、（﹣1）×2÷（﹣3） C、（﹣1）×（﹣2）÷（﹣3） D、（﹣1）÷2×0

查看试题解析
12. 在公园内，牡丹按正方形种植，在它的周围种植芍药，如图反映了牡丹的列数（n）和芍药的数量规律，那么当n=11时，芍药的数量为（）

A、84株 B、88株 C、92株 D、121株

查看试题解析

二、填空题

13. 下列说法：
①近似数3.9×10³精确到十分位；
②按科学记数法表示8.04×10⁵原数为80400；
③把数60430保留2个有效数字得6.0×10⁴；
④用四舍五入法得到的近似数9.1780是精确到0.001；
⑤近似数2.40万精确到百位，有3个有效数字．
其中正确的有个．

查看试题解析
14. 若将代数式中的任意两个字母交换，代数式不变，则称这个代数式为完全对称式，如a+b+c就是完全对称式，下列三个代数式：①a﹣b﹣c；②﹣a﹣b﹣c+2；③ab+bc+ca；④a²b+b²c+c²a，其中是完全对称式的是．

查看试题解析
15. 请你任意想一个数，把这个数乘2后减1，然后除以4，再减去你选来所想那个数的一半，你计算的结果是．

查看试题解析
16. 当a-b=-1，ab=-2时，-（a-2b+3ab）-[-（2a-3b-ab）]= ．

查看试题解析
17. 若|x﹣1|+|y+3|=0，则x﹣y= ．若|a|=21，|b|=27，且a＞b，则a﹣b= ．

查看试题解析
18. 杨辉是我国南宋时期杰出的数学家和教育家，如图是杨辉在公元1261年著作《详解九章算法》里面的一张图，即“杨辉三角”，该图中有很多规律，请仔细观察，解答下列问题：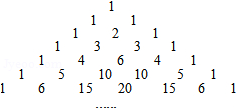

(1)、图中给出了七行数字，根据构成规律，第8行中从左边数第3个数是；

(2)、利用不完全归纳法探索出第n行中的所有数字之和为．

查看试题解析

三、解答题

19. 将下列各数填在相应的集合里：﹣32，0，0.24，﹣1 $\frac{2}{5}$ ，2700，﹣81，﹣ $\frac{6}{7}$ ，19%，﹣3²
整数集合{…}

分数集合{…}

负分数集合{…}．

查看试题解析
20. 当k为何值时，多项式4x^|2k^﹣1|y+xy﹣5是四次多项式？此时是关于x的几次式？

查看试题解析
21. 计算：

(1)、（﹣2）²+[18﹣（﹣3）×2]÷4．

(2)、﹣3（2x²y﹣3xy²+2）﹣（x²y﹣xy²+2）﹣x．

查看试题解析
22. 为了有效控制酒后驾车，吉安市城管的汽车在一条东西方向的公路上巡逻，如果规定向东为正，向西为负，从出发点开始所走的路程为：
+2，﹣3，+2，+1，﹣2，﹣1，﹣2（单位：千米）

(1)、此时，这辆城管的汽车司机如何向队长描述他的位置？

(2)、如果队长命令他马上返回出发点，这次巡逻（含返回）共耗油多少升？（已知每千米耗油0.2升）

查看试题解析
23. 已知 A=2x²﹣9x﹣11，B=﹣6x+3x²+4，且B+C=A

(1)、求多项式C；

(2)、求 $\frac{1}{2}$ A+2B的值．

查看试题解析
24.

(1)、已知代数式：4x﹣4xy+y²﹣x²y³
①将代数式按照y的次数降幂排列．

②当x=2，y=﹣1时，求该代数式的值

(2)、已知：关于xyz的代数式﹣（m+3）x²y^|m+1|z+（2m﹣n）x²y+5为五次二项式，求|m﹣n|的值．

查看试题解析
25. 已知数轴上A、B两点所表示的数分别为a和b．

(1)、如图，a=﹣1，b=7时

①求线段AB的长；

②若点P为数轴上与A、B不重合的动点，M为PA的中点，N为PB的中点，当点P在数轴上运动时，MN的长度是否发生改变？若不变，并求出线段MN的长；若改变，请说明理由．

(2)、不相等的有理数a、b、c在数轴上的对应点分别为A、B、Q，如果|a﹣c|﹣|b﹣c|=|a﹣b|，那么，Q点应在什么位置？请说明理由．

查看试题解析
26. 阅读材料，求值：1+2+2²+2³+2⁴+…+2²⁰¹⁵ ．
解：设S=1+2+2²+2³+2⁴+…+2²⁰¹⁵ ，将等式两边同时乘以2得：

2S=2+2²+2³+2⁴+…+2²⁰¹⁵+2²⁰¹⁶

将下式减去上式得2S﹣S=2²⁰¹⁶﹣1

即S=1+2+2²+2³+2⁴+…+2²⁰¹⁵=2²⁰¹⁶﹣1

请你仿照此法计算：

(1)、1+2+2²+2³+…+2¹⁰

(2)、1+3+3²+3³+3⁴+…+3ⁿ（其中n为正整数）

查看试题解析