沪科版九上数学23.2解直角三角形及其应用课时作业（4）
试卷更新日期：2020-04-13 类型：同步测试
一、选择题
-
1. 如图，一渔船由西往东航行，在A点测得海岛C位于北偏东 的方向，前进40海里到达B点，此时，测得海岛C位于北偏东 的方向，则海里C到航线AB的距离CD是（ ）
A、20海里 B、40海里 C、20 海里 D、40 海里2. 如图，一艘海轮位于灯塔P的北偏东方向55°，距离灯塔为2海里的点A处．如果海轮沿正南方向航行到灯塔的正东位置B处，海轮航行的距离AB长是（ ）
A、2海里 B、 海里 C、 海里 D、 海里3. 如图，一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号，继续在同一深度直线航行4000米后，在B处测得俯角为60°的海底也有该黑匣子发出的信号，则黑匣子所在位置点C在海面下的深度为（ ）
A、2000米 B、4000米 C、2000米 D、（2000 +500）米4. 上午9时，一条船从A处出发，以每小时40海里的速度向正东方向航行，9时30分到达B处（如图）．从A，B两处分别测得小岛M在北偏东45°和北偏东15°方向，那么在B处船与小岛M的距离为（ ）
A、20海里 B、20 海里 C、10 海里 D、20 海里5.如图，在A、B 两地之间要修一条笔直的公路，从A地测得公路走向是北偏东48°，A，B两地同时开工，若干天后公路准确接通，若公路AB长8千米，另一条公路BC长是6千米，且BC的走向是北偏西42°，则A地到公路BC的距离是（ ）
A、6千米 B、8千米 C、10千米 D、14千米6. 如图，马航370失联后，“海巡31”船匀速在印度洋搜救，当它行驶到A处时，发现它的北偏东 方向有一灯塔B，海巡船继续向北航行4小时后到达C处，发现灯塔B在它的北偏东 方向．若海巡船继续向北航行，那么要再过多少时间海巡船离灯塔B最近？（ ）
A、1小时 B、2小时 C、 小时 D、2 小时7. 如图，一艘海轮位于灯塔P的南偏东45°方向距离灯塔60海里的A处，它沿正北方向航行一段时间后，到达位于灯塔P的北偏东30°方向上的B处，这时，B处与灯塔P的距离为（ ）
A、60 海里 B、60 海里 C、30 海里 D、30 海里8. 如图，某轮船在点O处测得一个小岛上的电视塔A在北偏西60°的方向，船向西航行20海里到达B处，测得电视塔A在船的西北方向，若要轮船离电视塔最近，则还需向西航行（ ）
A、 海里 B、 海里 C、 海里 D、 海里二、填空题
-
9.
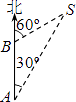
如图，一艘船向正北航行，在A处看到灯塔S在船的北偏东30°的方向上，航行12海里到达B点，在B处看到灯塔S在船的北偏东60°的方向上，此船继续沿正北方向航行过程中距灯塔S的最近距离是海里（不近似计算）．
10. 如图，一艘海轮位于灯塔P的北偏东方向60°，距离灯塔为4海里的点A处，如果海轮沿正南方向航行到灯塔的正东位置，海轮航行的距离AB长海里．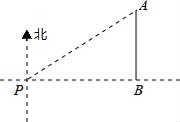
11. 一艘货轮以18 km/h的速度在海面上沿正东方向航行，当行驶至A处时，发现它的东南方向有一灯塔B，货轮继续向东航行30分钟后到达C处，发现灯塔B在它的南偏东15°方向，则此时货轮与灯塔B的距离是km．
12. “奔跑吧，兄弟！”节目组预设计一个新游戏：“奔跑”路线A，B，C，D四地，如图A，B，C三地在同一直线上，D在A北偏东30°方向，在C北偏西45°方向，C在A北偏东75°方向，且BD=BC=40m，从A地到D地的距离是m．
13. 如图．一艘渔船正以60海里/小时的速度向正东方向航行，在A处测得岛礁P在东北方向上，继续航行1.5小时后到达B处此时测得岛礁P在北偏东 方向，同时测得岛礁P正东方向上的避风港M在北偏东 方向为了在台风到来之前用最短时间到达M处，渔船立刻加速以75海里/小时的速度继续航行小时即可到达(结果保留根号)
14. 如图，一艘海轮位于灯塔P的北偏东60°方向，距离灯塔86n mile的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，此时B处与灯塔P的距离约为n mile.(结果取整数，参考数据： ＝1.7， ≈ 1.4)
15. 如图，已知一条东西走向的河流，在河流对岸有一点A，小明在岸边点B处测得点A在点B的北偏东30°方向上，小明沿河岸向东走80m后到达点C，测得点A在点C的北偏西60°方向上，则点A到河岸BC的距离为 ．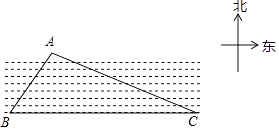
三、解答题
-
16.
如图，C地在A地的正东方向，因有大山阻隔，由A地到C地需绕行B地，已知B地位于A地北偏东67°方向，距离A地520km，C地位于B地南偏东30°方向，若打通穿山隧道，建成两地直达高铁，求A地到C地之间高铁线路的长．（结果保留整数）
（参考数据：sin67°≈ ，cos67°≈ ，tan67°≈ ， ≈1.73）
17. 如图，某市郊外景区内一条笔直的公路l经过A、B两个景点，景区管委会又开发了风景优美的景点C．经测量，C位于A的北偏东60°的方向上，C位于B的北偏东30°的方向上，且AB=10km．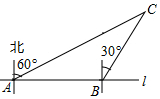
(1)、求景点B与C的距离；(2)、为了方便游客到景点C游玩，景区管委会准备由景点C向公路l修一条距离最短的公路，不考虑其他因素，求出这条最短公路的长．（结果保留根号）18.如图，专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处，同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上．已知B在A的正东方向，且相距100里，请分别求出两艘船到达事发地点C的距离．（注：里是海程单位，相当于一海里．结果保留根号）
19. 如图，自来水厂A和村庄B在小河1的两侧，现要在A，B间铺设一条输水管道，为了搞好工程预算，需测算出A，B间的距离
一小船在点P处测得A在正北方向，B位于南偏东 方向，前行1200m，到达点Q处，测得A位于北偏西 方向，B位于南偏西 方向． 
(1)、求BQ长度；(2)、求A，B间的距离(参考数据： )20. 如图，海面上甲、乙两船分别从A，B两处同时出发，由西向东行驶，甲船的速度为24n mile/h，乙船的速度为15n mile/h，出发时，测得乙船在甲船北偏东50°方向，且AB=10nmile，经过20分钟后，甲、乙两船分别到达C，D两处．（参考值：sin50°≈0.766，cos50°≈0.643，tan50°≈1.192）
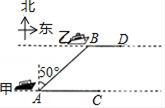(1)、求两条航线间的距离；(2)、若两船保持原来的速度和航向，还需要多少时间才能使两船的距离最短？（精确到0.01）21. 如图所示，位于A处的海上救援中心获悉：在其北偏东 方向的B处有一艘渔船遇险，在原地等待营救．该中心立即把消息告知在其北偏东 相距20海里的C处救生船，并通知救生船，遇险船在它的正东方向B处，现救生船沿着航线CB前往B处救援，若救生船的速度为20海里/时，请问：
(1)、C到AB的最短距离是多少？(2)、救生船到达B处大约需要多长时间？（结果精确到0.1小时：参考数据： ， ， ， ， ， ）