沪科版九上数学23.2解直角三角形及其应用课时作业(1)
试卷更新日期:2020-04-13 类型:同步测试
一、选择题
-
1. 如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为( )
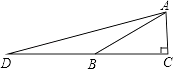 A、2+ B、2 C、3+ D、32. 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
A、2+ B、2 C、3+ D、32. 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )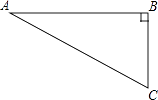 A、 B、 C、 D、3. 如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=8,tan∠ABD= ,则线段AB的长为( )
A、 B、 C、 D、3. 如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=8,tan∠ABD= ,则线段AB的长为( ) A、 B、2 C、5 D、104. 如图,在Rt△ABC中,∠ACB=90,CD⊥AB,垂足为D,若AC= , BC=2.则sin∠ACD的值为( )
A、 B、2 C、5 D、104. 如图,在Rt△ABC中,∠ACB=90,CD⊥AB,垂足为D,若AC= , BC=2.则sin∠ACD的值为( ) A、 B、 C、 D、5. 如图 ,在直角△BAD中,延长斜边BD到点C,使DC= BD,连结AC,若tanB= ,则tan∠CAD的值为 ( )
A、 B、 C、 D、5. 如图 ,在直角△BAD中,延长斜边BD到点C,使DC= BD,连结AC,若tanB= ,则tan∠CAD的值为 ( )
A、 B、 C、 D、6. 如图,若△ABC和△DEF的面积分别为S1 , S2 , 则( ) A、S1=S2 B、S1=S2 C、S1=S2 D、S1=S27. 如图,在等腰Rt△ABC中,∠C=90°,AC=3,D是AC上一点.若tan∠DBA= , 则AD的长为( )
A、S1=S2 B、S1=S2 C、S1=S2 D、S1=S27. 如图,在等腰Rt△ABC中,∠C=90°,AC=3,D是AC上一点.若tan∠DBA= , 则AD的长为( ) A、2 B、 C、 D、18. 如图,在▱ABCD中,AB:AD=3:2,∠ADB=60°,那么cos∠A的值等于( )
A、2 B、 C、 D、18. 如图,在▱ABCD中,AB:AD=3:2,∠ADB=60°,那么cos∠A的值等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,Rt△ABC中,∠C=90°,BC=15,tanA= ,则AB= .
 10. 如图,已知菱形ABCD,对角线AC,BD相交于点O.若tan∠BAC= ,AC=6,则BD的长是.
10. 如图,已知菱形ABCD,对角线AC,BD相交于点O.若tan∠BAC= ,AC=6,则BD的长是. 11. 已知Rt△ABC中,∠C=90°,∠A=60°,a-b=2,则c=.12. △ABC中,AB=12,AC= ,∠B=30°,则△ABC的面积是 .13. 如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(﹣1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ= ,那么当点P运动一周时,点Q运动的总路程为 .
11. 已知Rt△ABC中,∠C=90°,∠A=60°,a-b=2,则c=.12. △ABC中,AB=12,AC= ,∠B=30°,则△ABC的面积是 .13. 如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(﹣1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ= ,那么当点P运动一周时,点Q运动的总路程为 .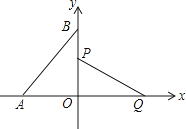 14. 如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM= AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是 ,则 的值是 .
14. 如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM= AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是 ,则 的值是 .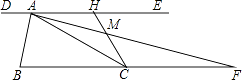
三、解答题
-
15. 如图,在Rt△ABC中,∠C=90°,sinA= ,D为AC上一点,∠BDC=45°,DC=6 cm,求AB、AD的长.
 16. 如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD= ,求sinC的值.
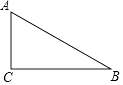
16. 如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD= ,求sinC的值. 17. 如图,在△ABC中,BC=12,tanA= ,∠B=30°;求AC和AB的长.
17. 如图,在△ABC中,BC=12,tanA= ,∠B=30°;求AC和AB的长. 18. 如图,若要在宽AD为20米的城南大道两边安装路灯,路灯的灯臂BC长2米,且与灯柱AB成120°角,路灯采用圆锥形灯罩,灯罩的轴线CO与灯臂BC垂直,当灯罩的轴线CO通过公路路面的中心线时照明效果最好,此时,路灯的灯柱AB高应该设计为多少米(结果保留根号)?
18. 如图,若要在宽AD为20米的城南大道两边安装路灯,路灯的灯臂BC长2米,且与灯柱AB成120°角,路灯采用圆锥形灯罩,灯罩的轴线CO与灯臂BC垂直,当灯罩的轴线CO通过公路路面的中心线时照明效果最好,此时,路灯的灯柱AB高应该设计为多少米(结果保留根号)? 19. 如图,BD是△ABC的角平分线,点E,F分别在BC、AB上,且DE∥AB,EF∥AC.
19. 如图,BD是△ABC的角平分线,点E,F分别在BC、AB上,且DE∥AB,EF∥AC. (1)、求证:BE=AF;(2)、若∠ABC=60°,BD=6,求四边形ADEF的面积.20. 如图,根据图中数据完成填空,再按要求答题:
(1)、求证:BE=AF;(2)、若∠ABC=60°,BD=6,求四边形ADEF的面积.20. 如图,根据图中数据完成填空,再按要求答题: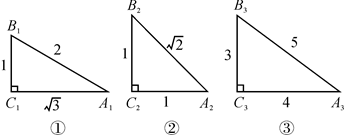 (1)、sin2A1+sin2B1=;sin2A2+sin2B2=;sin2A3+sin2B3=;(2)、观察上述等式,猜想:在Rt△ABC中,∠C=90°.都有:sin2A+sin2B=;(3)、如图,在Rt△ABC中,∠C=90°,∠A , ∠B , ∠C的对边分别是a , b , c;利用三角函数的定义和勾股定理,证明你的猜想;
(1)、sin2A1+sin2B1=;sin2A2+sin2B2=;sin2A3+sin2B3=;(2)、观察上述等式,猜想:在Rt△ABC中,∠C=90°.都有:sin2A+sin2B=;(3)、如图,在Rt△ABC中,∠C=90°,∠A , ∠B , ∠C的对边分别是a , b , c;利用三角函数的定义和勾股定理,证明你的猜想;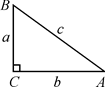 (4)、已知:∠A+∠B=90°,且sinA= , 求sinB.
(4)、已知:∠A+∠B=90°,且sinA= , 求sinB.