沪科版九上数学23.1锐角的三角函数课时作业（2）

试卷更新日期：2020-04-13 类型：同步测试

进入出卷网下载

一、选择题

1. 在 $R t △ A B C$ 中， $∠ A = 90 °$ ， $A B = 3$ ， $B C = 4$ ，则 $\cos B$ =（）

A、 $\frac{3}{4}$ B、 $\frac{\sqrt{7}}{4}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
2. 在Rt△ABC中，∠C=90°，AB=5，AC=4，则sinA等于（　　）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
3. 在△ABC中，∠C＝90°，AC= $\sqrt{2}$ ，AB= $\sqrt{5}$ ，则cosB的值为（）

A、 $\frac{\sqrt{10}}{2}$ B、 $\frac{\sqrt{10}}{5}$ C、 $\frac{\sqrt{15}}{5}$ D、 $\frac{3 \sqrt{15}}{5}$

查看试题解析
4. 如图，在Rt△ABC中，∠C=90°，BC=4，AC=3，则sinB= $\frac{A C}{A B}$ =（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{3}{7}$ D、 $\frac{3}{4}$

查看试题解析
5. 如图，在Rt△ABC中，CD是斜边AB上的高，∠A≠45°，则下列比值中不等于cosA的是（）

A、 $\frac{BD}{CB}$ B、 $\frac{CD}{CB}$ C、 $\frac{AC}{AB}$ D、 $\frac{AD}{AC}$

查看试题解析
6. 如图CD是Rt△ABC斜边上的高，AC=4，BC=3，则cos∠BCD的值是（）

A、 $\frac{4}{5}$ B、 $\frac{3}{4}$ C、 $\frac{4}{3}$ D、 $\frac{3}{5}$

查看试题解析
7. 等腰三角形的底边长10cm，周长36cm，则底角的余弦值为（）

A、 $\frac{5}{12}$ B、 $\frac{12}{5}$ C、 $\frac{5}{13}$ D、 $\frac{12}{13}$

查看试题解析
8. 在Rt△ABC中，∠C=90°，∠B=35°，AB=7，则BC的长为（）

A、 $\frac{7}{\cos 35 °}$ B、7sin55° C、cos55° D、tan55°

查看试题解析

二、填空题

9. 在以O为坐标原点的直角平面内有一点A(2,4)，如果AO与x轴正半轴的夹角为a，那么a的余弦值为.

查看试题解析
10. 在△ABC中，∠C=90°，AB=10，BC=8，则cos A= ．

查看试题解析
11. 在Rt△ABC中，∠C=90°，AB=3，BC=2，则cosA的值是.

查看试题解析
12. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $BC = 3$ ， $AC = 4$ ，那么 $cosA =$ .

查看试题解析
13. 已知△ABC中，∠C=90°，a= $5 \sqrt{3}$ ，∠B=30°,则c=.

查看试题解析
14. 如图，方格纸中有三个格点A，B，C，则sin∠ABC=.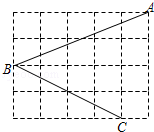

查看试题解析
15. 如图，在长和宽分别是8和7矩形内，放置了如图中5个大小相同的正方形，则正方形的边长是.

查看试题解析

三、解答题

16. 等腰三角形周长为16，一边长为6，求底角的余弦值.

查看试题解析
17. 已知：如图，在Rt $△ A B C$ 中，∠ACB=90°，点D是斜边AB上的一点，且CD=AC=3，AB=4，求cosB，sin∠ADC及cos $\frac{1}{2}$ ∠DCA的值．

查看试题解析
18. 如图，△ABC中，AB＝BC．

(1)、用直尺和圆规作△ABC的中线BD；（不要求写作法，保留作图痕迹）；

(2)、在（1）的条件下，若BC＝6，BD＝4，求 $cosA$ 的值.

查看试题解析
19. 如图，将△ABC沿着射线BC方向平移至△A′B′C′，使点A′落在∠ACB的外角平分线CD上，连结AA′．

(1)、判断四边形ACC′A′的形状，并说明理由；

(2)、在△ABC中，∠B=90°，AB=8，cos∠BAC= $\frac{4}{5}$ ，求CB′的长．

查看试题解析
20. 如图，在矩形ABCD中，DE⊥AC于E， $cos ∠ A D E = \frac{3}{5}$ ，AB＝3，

(1)、求AD的值；

(2)、直接写出 $S_{Δ D E C}$ 的值

查看试题解析
21. 如图，平行四边形ABCD在平面直角坐标系中，AD=6，若OA、OB的长是关于x的一元二次方程 $x^{2} - 7 x + 12 = 0$ 的两个根，且OA＞OB

(1)、求cos∠ABC的值。

(2)、若E为轴上的点，且 $S_{△ A O E} = \frac{16}{3}$ ，求出点E的坐标，并判断△AOE与△DAO是否相似？请说明理由。

查看试题解析