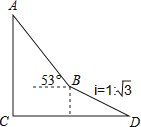沪科版九上数学23.1锐角的三角函数课时作业(1)
试卷更新日期:2020-04-13 类型:同步测试
一、选择题
-
1. 在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠A的正切值为( )A、3 B、 C、 D、2. 如图,修建抽水站时,沿着坡度为i=1:6的斜坡铺设管道. 下列等式成立的是( )
 A、sinα = B、cosα= C、tanα= D、tanα=23. 如图,在Rt△ABC中,∠C=90°,∠A=30°,c=10,则下列错误的是( )
A、sinα = B、cosα= C、tanα= D、tanα=23. 如图,在Rt△ABC中,∠C=90°,∠A=30°,c=10,则下列错误的是( ) A、∠B=60° B、a=5 C、b=5 D、tan B=4.
A、∠B=60° B、a=5 C、b=5 D、tan B=4.如图,已知在Rt△ABC中,∠C=90°,AC=4,tanA= , 则AB的长是( )
 A、2 B、8 C、2 D、45. 如图,在Rt△ABC中,∠C=90°,点B在CD上,且BD=BA=2AC,则tan∠DAC的值为( )
A、2 B、8 C、2 D、45. 如图,在Rt△ABC中,∠C=90°,点B在CD上,且BD=BA=2AC,则tan∠DAC的值为( ) A、2+ B、2 C、3+ D、36. 如图,A,B,C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为( )
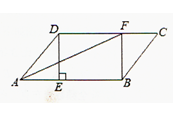
A、2+ B、2 C、3+ D、36. 如图,A,B,C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为( )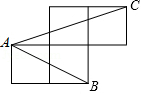 A、 B、1 C、 D、7. 如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )
A、 B、1 C、 D、7. 如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )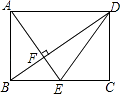 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
8. 在 中, 为直角, 、∠B、∠C所对的边分别为a、B、c,且 , ,则tan∠B = .9. 如图,在直角坐标系中放入一个边长OC为9的矩形纸片ABCO.将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知tan∠OB′C= .则点B′点的坐标为 .
 10. 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AC=4,BC=3,则∠DCB的正切值为.
10. 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AC=4,BC=3,则∠DCB的正切值为. 11. 如图所示,直角梯形ABCD中,AB⊥BC,AD∥BC,BC>AD,AD=2,AB=4,点E在AB上,将△CBE沿CE翻折,使B点与D点重合,则∠BCE的正切值是 .
11. 如图所示,直角梯形ABCD中,AB⊥BC,AD∥BC,BC>AD,AD=2,AB=4,点E在AB上,将△CBE沿CE翻折,使B点与D点重合,则∠BCE的正切值是 . 12. 如图,在顶角为30°的等腰三角形ABC中,AB=AC,若过点C作CD⊥AB于点D,则∠BCD=15°,根据图形计算tan15°= .
12. 如图,在顶角为30°的等腰三角形ABC中,AB=AC,若过点C作CD⊥AB于点D,则∠BCD=15°,根据图形计算tan15°= . 13. 如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则tan∠AOD=.
13. 如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则tan∠AOD=.
三、解答题
-
14. 在等腰直角三角形ABC中,∠C=90°,AC=10,D是AC上一点,若tan∠DBC= ,求AD的长.15. 如图,在Rt△ABC中,∠ACB=900 , CD⊥AB于D,tan∠ABC= ,且BC=9cm,求AC,AB及CD的长.
 16. 小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为 , 已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度(结果保留整数)
16. 小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为 , 已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度(结果保留整数)(参考数据: , ,
 17.
17.如图,为了测量出楼房AC的高度,从距离楼底C处60 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1: 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈ ,计算结果用根号表示,不取近似值).